【题目】已知函数f(x)=loga ![]() ,(a>0且a≠1).
,(a>0且a≠1).
(1)判断f(x)的奇偶性,并加以证明;
(2)是否存在实数m使得f(x+2)+f(m﹣x)为常数?若存在,求出m的值;若不存在,说明理由.
参考答案:
【答案】
(1)
解:f(x)=loga ![]() 为奇函数,下面证明:
为奇函数,下面证明:
解 ![]() >0可得定义域为{x|x<﹣5或x>5},关于原点对称,
>0可得定义域为{x|x<﹣5或x>5},关于原点对称,
f(﹣x)=loga ![]() =﹣loga
=﹣loga ![]() =﹣f(x),
=﹣f(x),
∴函数f(x)为奇函数
(2)
解:假设存在这样的m,则f(x+2)+f(m﹣x)
=loga ![]()
![]() =loga
=loga ![]() ,
,
∴ ![]() 为常数,设为k,
为常数,设为k,
则(k﹣1)x2+(m﹣2)(1﹣k)x﹣3(m﹣5)﹣7k(m+5)=0对定义域内的x恒成立
∴ 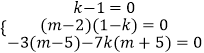 ,解得
,解得 ![]()
∴存在这样的m=﹣2
【解析】(1)f(x)=loga ![]() 为奇函数,求函数的定义域并利用奇函数的定义证明即可;(2)假设存在这样的m,则f(x+2)+f(m﹣x)=loga
为奇函数,求函数的定义域并利用奇函数的定义证明即可;(2)假设存在这样的m,则f(x+2)+f(m﹣x)=loga ![]() ,即
,即 ![]() 为常数,设为k,整理由多项式系数相等可得m和k的方程组,解方程组可得.
为常数,设为k,整理由多项式系数相等可得m和k的方程组,解方程组可得.
【考点精析】本题主要考查了函数的奇函数的相关知识点,需要掌握一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=—f(x),那么f(x)就叫做奇函数才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知X和Y是两个分类变量,由公式K2=
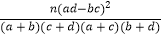 算出K2的观测值k约为7.822根据下面的临界值表可推断( )
算出K2的观测值k约为7.822根据下面的临界值表可推断( ) P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828
A.推断“分类变量X和Y没有关系”犯错误的概率上界为0.010
B.推断“分类变量X和Y有关系”犯错误的概率上界为0.010
C.有至少99%的把握认为分类变量X和Y没有关系
D.有至多99%的把握认为分类变量X和Y有关系 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x2﹣4x+a,g(x)=logax(a>0且a≠1).
(1)若函数f(x)在[﹣1,2m]上不具有单调性,求实数m的取值范围;
(2)若f(1)=g(1).
(ⅰ)求实数a的值;
(ⅱ)设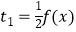 ,t2=g(x),
,t2=g(x), 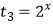 ,当x∈(0,1)时,试比较t1 , t2 , t3的大小.
,当x∈(0,1)时,试比较t1 , t2 , t3的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范围;
(2)当x∈[0,+∞)时,求函数y=g(x)﹣f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】一种计算装置,有一数据入口A和一个运算出口B,按照某种运算程序:①当从A口输入自然数1时,从B口得到
 ,记为
,记为 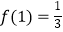 ;②当从A口输入自然数n(n≥2)时,在B口得到的结果f(n)是前一个结果f(n﹣1)的
;②当从A口输入自然数n(n≥2)时,在B口得到的结果f(n)是前一个结果f(n﹣1)的 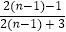 倍. (Ⅰ)当从A口分别输入自然数2,3,4时,从B口分别得到什么数?
倍. (Ⅰ)当从A口分别输入自然数2,3,4时,从B口分别得到什么数?
(Ⅱ)根据(Ⅰ)试猜想f(n)的关系式,并用数学归纳法证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的程序框图表示求式子1×3×7×15×31×63的值,则判断框内可以填的条件为( )
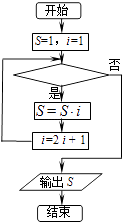
A.i≤31?
B.i≤63?
C.i≥63?
D.i≤127? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,
 <φ<π)部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为
<φ<π)部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为  ,则f(﹣1)=( )
,则f(﹣1)=( ) 
A.﹣2
B.2
C.-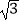
D.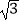
相关试题

