【题目】已知 ![]() =(sinx,sin(x﹣
=(sinx,sin(x﹣ ![]() )),
)), ![]() =(sinx,cos(x+
=(sinx,cos(x+ ![]() )),f(x)=
)),f(x)= ![]()
![]() .
.
(1)求f(x)的解析式及周期;
(2)求f(x)在x∈[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
参考答案:
【答案】
(1)解:f(x)=sin2x+sin(x﹣ ![]() )cos(x+
)cos(x+ ![]() )=sin2x﹣sin2(x-
)=sin2x﹣sin2(x- ![]() )
)
= ![]() ﹣
﹣ 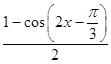 =
= ![]() [cos(2x﹣
[cos(2x﹣ ![]() )﹣cos2x]
)﹣cos2x]
= ![]() (
( ![]() sin2x﹣
sin2x﹣ ![]() cos2x)=
cos2x)= ![]() sin(2x﹣
sin(2x﹣ ![]() ).
).
∴f(x)的周期T= ![]() =π
=π
(2)解:∵x∈[﹣ ![]() ,
, ![]() ],∴2x﹣
],∴2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴当2x﹣ ![]() =﹣
=﹣ ![]() 时,f(x)取得最小值
时,f(x)取得最小值 ![]() =﹣
=﹣ ![]() .
.
当2x﹣ ![]() =
= ![]() 时,f(x)取得最大值
时,f(x)取得最大值 ![]() =
= ![]()
∴f(x)在x∈[﹣ ![]() ,
, ![]() ]上的值域是[﹣
]上的值域是[﹣ ![]() ,
, ![]() ]
]
【解析】(1)利用向量的数量积公式得出f(x),利用二倍角公式,诱导公式及两角和差的三角函数化简;(2)根据x的范围得出2x﹣ ![]() 的范围,根据正弦函数的单调性得出f(x)的最值.
的范围,根据正弦函数的单调性得出f(x)的最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,圆心为
,圆心为 ,定点
,定点 ,
,  为圆
为圆 上一点,线段
上一点,线段 上一点
上一点 满足
满足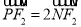 ,直线
,直线 上一点
上一点 ,满足
,满足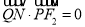 .
.(Ⅰ)求点
 的轨迹
的轨迹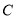 的方程;
的方程;(Ⅱ)
 为坐标原点,
为坐标原点,  是以
是以 为直径的圆,直线
为直径的圆,直线 与
与 相切,并与轨迹
相切,并与轨迹 交于不同的两点
交于不同的两点 .当
.当 且满足
且满足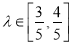 时,求
时,求 面积
面积 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知袋中装有大小相同的2个白球、2个红球和1个黄球.一项游戏规定:每个白球、红球和黄球的分值分别是0分、1分和2分,每一局从袋中一次性取出三个球,将3个球对应的分值相加后称为该局的得分,计算完得分后将球放回袋中.当出现第
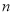 局得
局得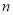 分(
分(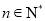 )的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
)的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.(1)求在一局游戏中得3分的概率;
(2)求游戏结束时局数
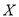 的分布列和数学期望
的分布列和数学期望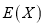 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某科研小组研究发现:一棵水蜜桃树的产量
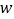 (单位:百千克)与肥料费用
(单位:百千克)与肥料费用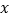 (单位:百元)满足如下关系:
(单位:百元)满足如下关系: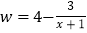 ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)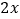 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为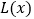 (单位:百元).
(单位:百元).(1)求利润函数
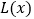 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某医学院读书协会欲研究昼夜温差大小与患感冒人数多少之间的关系,该协会分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如图所示的频率分布直方图.该协会确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.

(Ⅰ)已知选取的是1月至6月的两组数据,请根据2至5月份的数据,求出就诊人数
 关于昼夜温差
关于昼夜温差 的线性回归方程;
的线性回归方程;(Ⅱ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问(Ⅰ)中该协会所得线性回归方程是否理想?
参考公式:回归直线的方程
 ,
,其中
 ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,甲船以每小时30
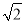 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10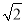 海里.问:乙船每小时航行多少海里?
海里.问:乙船每小时航行多少海里?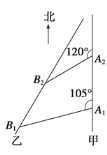
-
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}满足a3=5,a10=-9.
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn及使得Sn最大的序号n的值.
相关试题

