【题目】已知中心在原点的椭圆C的左焦点F(﹣ ![]() ,0),右顶点A(2,0).
,0),右顶点A(2,0).
(1)求椭圆C的标准方程;
(2)斜率为 ![]() 的直线l与椭圆C交于A、B两点,求弦长|AB|的最大值及此时l的直线方程.
的直线l与椭圆C交于A、B两点,求弦长|AB|的最大值及此时l的直线方程.
参考答案:
【答案】
(1)解:由题意可知:c= ![]() ,a=2,∴b2=a2﹣c2=1.
,a=2,∴b2=a2﹣c2=1.
∵焦点在x轴上,
∴椭圆C的方程为: ![]()
(2)解:设直线l的方程为y= ![]() x+b,由
x+b,由 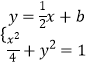 ,
,
可得x2+2bx+2b2﹣2=0,
∵l与椭圆C交于A、B两点,
∴△=4b2﹣4(2b2﹣2)≥0,即b2≤2.
设A(x1,y1),B(x2,y2),
则x1+x2=﹣2b,x1x2=2b2﹣2.
∴弦长|AB|= ![]() =
= ![]() ,
,
∵0≤b2≤2,
∴|AB|= ![]() ≤
≤ ![]() ,
,
∴当b=0,即l的直线方程为y= ![]() x时,弦长|AB|的最大值为
x时,弦长|AB|的最大值为 ![]()
【解析】(1)由已知根据椭圆的简单性质可求出a、b的值进而得到椭圆的方程。(2)联立直线和椭圆的方程得到关于x的一元二次方程,设出A、B两点的坐标根据韦达定理得到x1+x2和x1x2 关系式,代入弦长公式即可求出结果,利用椭圆自身的范围限制得到b的取值范围,进而得到弦长|AB|的最大值以及直线的方程。
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
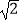 .
.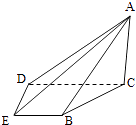
(Ⅰ)证明:AC⊥平面BCDE;
(Ⅱ)求直线AE与平面ABC所成的角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
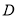 上的函数
上的函数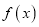 ,如果满足:对任意
,如果满足:对任意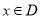 ,存在常数
,存在常数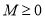 ,都有
,都有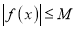 成立,则称
成立,则称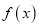 是
是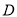 上的有界函数,其中
上的有界函数,其中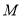 称函数
称函数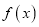 的一个上界.已知函数
的一个上界.已知函数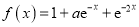 ,
, 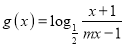 .
.(1)若函数
 为奇函数,求实数
为奇函数,求实数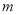 的值;
的值;(2)在第(1)的条件下,求函数
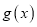 在区间
在区间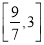 上的所有上界构成的集合;
上的所有上界构成的集合;(3)若函数
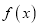 在
在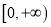 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数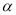 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,点
中,点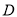 是
是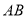 的中点.
的中点.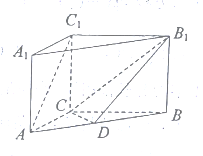
(1)求证:
 平面
平面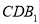 ;
;(2)若
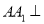 平面
平面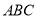 ,
, 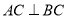 ,
, 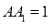 ,
, 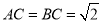 ,求二面角
,求二面角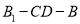 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】设F1 , F2分别是C:
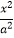 +
+ 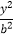 =1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
=1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为 ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
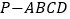 的底面
的底面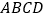 是菱形,
是菱形,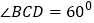 ,
,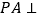 平面
平面 ,
, 是
是 的中点.
的中点.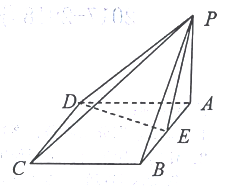
(1)求证:平面
 平面
平面 ;
;(2)棱
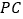 上是否存在一点
上是否存在一点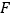 ,使得
,使得 平面
平面 ?若存在,确定
?若存在,确定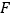 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别为CC1和BB1的中点,则异面直线AE与D1F所成角的余弦值为( )

A.0
B.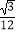
C.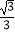
D.
相关试题

