【题目】如图,四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点.
的中点.
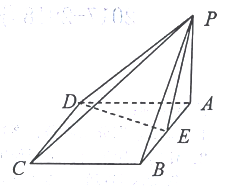
(1)求证:平面![]() 平面
平面![]() ;
;
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定
?若存在,确定![]() 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由.
参考答案:
【答案】(1)见解析(2) 点![]() 为
为![]() 的中点
的中点
【解析】试题分析:(1)证面面垂直,可先由线面垂直入手即![]() ,进而得到面面垂直;(2)通过构造平行四边形,得到线面平行。
,进而得到面面垂直;(2)通过构造平行四边形,得到线面平行。
解析:
(1)连接![]() ,因为底面
,因为底面![]() 是菱形,
是菱形,![]() ,所以
,所以![]() 为正三角形.
为正三角形.
因为![]() 是
是![]() 的中点, 所以
的中点, 所以![]() ,
,
因为![]() 面
面![]() ,
,![]() ,∴
,∴![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
又![]() , 所以面
, 所以面![]() ⊥面
⊥面![]() .
.
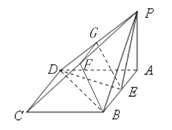
(2)当点![]() 为
为![]() 的中点时,
的中点时,![]() ∥面
∥面![]() .
.
事实上,取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,
∵![]() 为三角形
为三角形![]() 的中位线,
的中位线,
∴![]() ∥
∥![]() 且
且![]() ,
,
又在菱形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,
∴![]() ∥
∥![]() 且
且![]() ,
,
∴![]() ∥
∥![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形.
为平行四边形.
所以 ![]() ∥
∥![]() ,
,
又![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∴![]() ∥面
∥面![]() ,结论得证.
,结论得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,点
中,点 是
是 的中点.
的中点.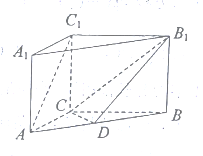
(1)求证:
 平面
平面 ;
;(2)若
 平面
平面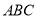 ,
, 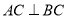 ,
, 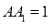 ,
, 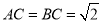 ,求二面角
,求二面角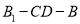 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点的椭圆C的左焦点F(﹣
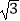 ,0),右顶点A(2,0).
,0),右顶点A(2,0).
(1)求椭圆C的标准方程;
(2)斜率为 的直线l与椭圆C交于A、B两点,求弦长|AB|的最大值及此时l的直线方程.
的直线l与椭圆C交于A、B两点,求弦长|AB|的最大值及此时l的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设F1 , F2分别是C:
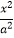 +
+ 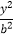 =1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
=1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为 ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别为CC1和BB1的中点,则异面直线AE与D1F所成角的余弦值为( )

A.0
B.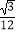
C.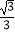
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一块形状为四棱柱的木料,
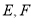 分别为
分别为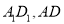 的中点.
的中点.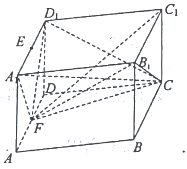
(1)要经过
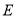 和
和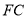 将木料锯开,在木料上底面
将木料锯开,在木料上底面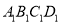 内应怎样画线?请说明理由;
内应怎样画线?请说明理由;(2)若底面
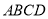 是边长为2的菱形,
是边长为2的菱形, 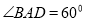 ,
, 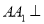 平面
平面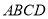 ,且
,且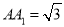 ,求几何体
,求几何体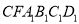 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市郊区有一加油站,2018年初汽油的存储量为50吨,计划从年初起每周初均购进汽油
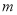 吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前
吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前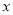 个周需求量
个周需求量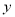 吨与
吨与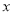 的函数关系式为
的函数关系式为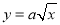
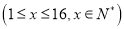 ,
, 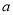 为常数,且前4个周城区内汽车的汽油需求量为100吨.
为常数,且前4个周城区内汽车的汽油需求量为100吨.(1)试写出第
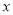 个周结束时,汽油存储量
个周结束时,汽油存储量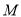 (吨)与
(吨)与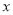 的函数关系式;
的函数关系式;(2)要使16个周内每周按计划购进汽油之后,加油站总能满足城区内和城外的需求,且每周结束时加油站的汽油存储量不超过150吨,试确定
 的取值范围.
的取值范围.
相关试题

