【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称函数
称函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在第(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:
(1)由函数为奇函数可得![]() ,即
,即![]() ,整理得
,整理得![]() ,可得
,可得![]() ,解得
,解得![]() ,经验证
,经验证![]() 不合题意.(2)根据单调性的定义可证明函数
不合题意.(2)根据单调性的定义可证明函数![]() 在区间
在区间![]() 上为增函数,从而可得
上为增函数,从而可得![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,故
,故![]() ,从而可得所有上界构成的集合为
,从而可得所有上界构成的集合为![]() .(3)将问题转化为
.(3)将问题转化为![]() 在
在![]() 上恒成立,整理得
上恒成立,整理得![]() 在
在![]() 上恒成立,通过判断函数的单调性求得
上恒成立,通过判断函数的单调性求得![]() 即可得到结果.
即可得到结果.
试题解析:
(1)∵函数![]() 是奇函数,
是奇函数,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
当![]() 时,
时, ![]() ,不合题意,舍去.
,不合题意,舍去.
∴![]() .
.
(2)由(1)得![]() ,
,
设![]() ,
,
令![]() ,且
,且![]() ,
,
∵![]()
![]() ;
;
∴![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() 在
在![]() 上是单调递增函数,
上是单调递增函数,
∴![]() 在区间
在区间![]() 上是单调递增,
上是单调递增,
∴![]() ,即
,即![]() ,
,
∴![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
∴![]() ,
,
故函数![]() 在区间
在区间![]() 上的所有上界构成的集合为
上的所有上界构成的集合为![]() .
.
(3)由题意知, ![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() ,
,
∴![]() ,
,
因此![]() 在
在![]() 上恒成立,
上恒成立,
∴![]()
设![]() ,
, ![]() ,
, ![]() ,由
,由![]() 知
知![]() ,
,
设![]() ,则
,则
![]() ,
, ![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减, ![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
, ![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
∴![]() .
.
∴![]() 的取值范围
的取值范围![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
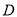 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意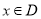 ,存在常数
,存在常数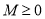 ,都有
,都有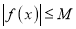 成立,则称
成立,则称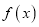 是
是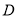 上的有界函数,其中
上的有界函数,其中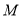 称函数
称函数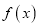 的一个上界.已知函数
的一个上界.已知函数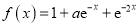 ,
, 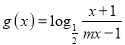 .
.(1)若函数
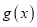 为奇函数,求实数
为奇函数,求实数 的值;
的值;(2)在第(1)的条件下,求函数
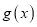 在区间
在区间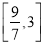 上的所有上界构成的集合;
上的所有上界构成的集合;(3)若函数
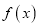 在
在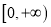 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数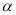 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线过点P(﹣3
 ,4),它的渐近线方程为y=±
,4),它的渐近线方程为y=±  x.
x.
(1)求双曲线的标准方程;
(2)设F1和F2为该双曲线的左、右焦点,点P在此双曲线上,且|PF1||PF2|=41,求∠F1PF2的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
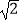 .
.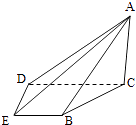
(Ⅰ)证明:AC⊥平面BCDE;
(Ⅱ)求直线AE与平面ABC所成的角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,点
中,点 是
是 的中点.
的中点.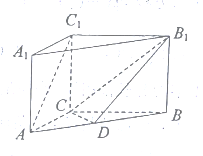
(1)求证:
 平面
平面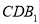 ;
;(2)若
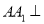 平面
平面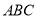 ,
, 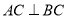 ,
, 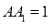 ,
, 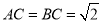 ,求二面角
,求二面角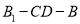 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点的椭圆C的左焦点F(﹣
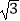 ,0),右顶点A(2,0).
,0),右顶点A(2,0).
(1)求椭圆C的标准方程;
(2)斜率为 的直线l与椭圆C交于A、B两点,求弦长|AB|的最大值及此时l的直线方程.
的直线l与椭圆C交于A、B两点,求弦长|AB|的最大值及此时l的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设F1 , F2分别是C:
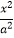 +
+ 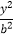 =1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
=1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为 ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
相关试题

