【题目】如图,直三棱柱![]() 中,底面是边长为2的正三角形,侧棱长为
中,底面是边长为2的正三角形,侧棱长为![]() ,
,![]() 为
为![]() 的中点
的中点
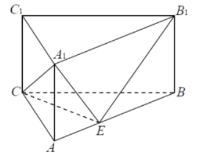
(1)若![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
参考答案:
【答案】(1)详见解析(2)![]()
【解析】
(1)本题首先可通过![]() 为
为![]() 的中点得出
的中点得出![]() ,然后根据三棱柱
,然后根据三棱柱![]() 是直棱柱得出
是直棱柱得出![]() 平面
平面![]() 以及
以及![]() ,再然后由
,再然后由![]() 得出
得出![]() ,最后根据
,最后根据![]() 即可证得
即可证得![]() 平面
平面![]() ;
;
(2)首先可以过点![]() 作
作![]() 平面
平面![]() ,然后根据线面角的相关性质可知
,然后根据线面角的相关性质可知![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,最后通过等体积法即可求得
所成的角,最后通过等体积法即可求得![]() 以及线面角的正弦值。
以及线面角的正弦值。
(1)因为△![]() 是正三角形,
是正三角形,![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为三棱柱![]() 是直棱柱,所以
是直棱柱,所以![]() 平面
平面![]() ,从而
,从而![]()
因为四边形![]() 是矩形,且
是矩形,且![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() 。
。
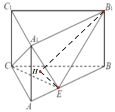
(2)如图所示,过点![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,则
,则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
在![]() 中,
中,![]() ,所以
,所以![]() .
.
在![]() 中,
中,![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
所以![]() ,解得
,解得![]() .
.
所以![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
(2)已知函数f(x)=ax2+2x是奇函数,则实数a=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列函数的奇偶性:
(1)f(x)=x+1;
(2)f(x)=x3+3x,x∈[-4,4);
(3)f(x)=|x-2|-|x+2|;
(4)f(x)=

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知长度为
 的线段
的线段 的两个端点
的两个端点 、
、 分别在
分别在 轴和
轴和 轴上运动,动点
轴上运动,动点 满足
满足 ,设动点
,设动点 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程;
的方程;(2)过点
 且斜率不为零的直线
且斜率不为零的直线 与曲线
与曲线 交于两点
交于两点 、
、 ,在
,在 轴上是否存在定点
轴上是否存在定点 ,使得直线
,使得直线 与
与 的斜率之积为常数.若存在,求出定点
的斜率之积为常数.若存在,求出定点 的坐标以及此常数;若不存在,请说明理由.
的坐标以及此常数;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】世界那么大,我想去看看,每年高考结束后,处于休养状态的高中毕业生旅游动机强烈,旅游可支配收入日益增多,可见高中毕业生旅游是一个巨大的市场.为了解高中毕业生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某市的1000名毕业生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别
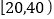

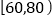
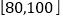
频数
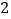
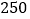
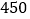
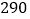
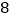
(1)求所得样本的中位数(精确到百元);
(2)根据样本数据,可近似地认为学生的旅游费用支出
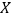 服从正态分布
服从正态分布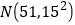 ,若该市共有高中毕业生35000人,试估计有多少位同学旅游费用支出在 8100元以上;
,若该市共有高中毕业生35000人,试估计有多少位同学旅游费用支出在 8100元以上;(3)已知本数据中旅游费用支出在
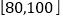 范围内的8名学生中有5名女生,3名男生, 现想选其中3名学生回访,记选出的男生人数为
范围内的8名学生中有5名女生,3名男生, 现想选其中3名学生回访,记选出的男生人数为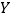 ,求
,求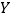 的分布列与数学期望.
的分布列与数学期望.附:若
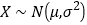 ,则
,则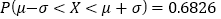 ,
,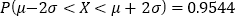 ,
,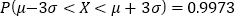 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列函数的奇偶性:
(1)f(x)=|x-2|+|x+2|;
(2)
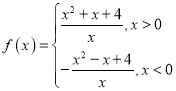
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面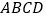 是平行四边形,
是平行四边形, 平面
平面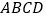 ,
, ,
, ,
,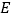 是棱
是棱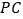 上的一点.
上的一点.(1)证明:
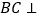 平面
平面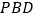 ;
; (2)若
 平面
平面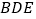 ,求
,求 的值;
的值;(3)在(2)的条件下,三棱锥
 的体积是18,求
的体积是18,求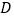 点到平面
点到平面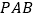 的距离.
的距离.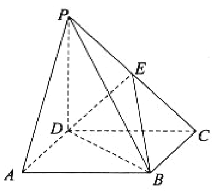
相关试题

