【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式:
参考答案:
【答案】(1) y=0.7x+0.35;(2) 19.65吨.
【解析】
(1)利用回归直线方程计算公式,计算出回归直线方程.(2)令![]() ,求得改造后的能耗,用原来的能耗减去改造后的能耗,求得生产能耗比技改前降低的标准煤吨数.
,求得改造后的能耗,用原来的能耗减去改造后的能耗,求得生产能耗比技改前降低的标准煤吨数.
(1)由对照数据,计算得![]() ,
,![]() =4.5,
=4.5,![]() =3.5,
=3.5,
∴回归方程的系数为![]() =0.7,
=0.7,![]() =3.5-0.7×4.5=0.35,
=3.5-0.7×4.5=0.35,
∴所求线性回归方程为y=0.7x+0.35;
(2)由(1)求出的线性回归方程,
估计生产100吨甲产品的生产能耗为0.7×100+0.35=70.35(吨),
由90-70.35=19.65,
∴生产100吨甲产品的生产能耗比技改前降低19.65吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文体局为了解“跑团”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是( )

A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.

(1)分别计算这10名同学中,男女生测试的平均成绩;
(2)若这10名同学中,男生和女生的国学素养测试成绩的标准差分别为S1,S2,试比较S1与S2的大小(不必计算,只需直接写出结果);
(3)规定成绩大于等于75分为优良,从这10名同学中随机选取一男一女两名同学,求这两名同学的国学素养测试成绩均为优良的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)若函数
 的图像与
的图像与 轴无交点,求
轴无交点,求 的取值范围;
的取值范围;(2)若方程
 在区间
在区间 上存在实根,求
上存在实根,求 的取值范围;
的取值范围;(3)设函数
 ,
, ,当
,当 时若对任意的
时若对任意的 ,总存在
,总存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
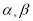 表示两个不同的平面,
表示两个不同的平面, 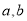 表示两条不同直线,对于下列两个命题:
表示两条不同直线,对于下列两个命题:①若
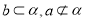 ,则“
,则“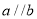 ”是“
”是“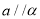 ”的充分不必要条件;
”的充分不必要条件;②若
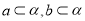 ,则“
,则“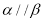 ”是“
”是“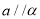 且
且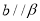 ”的充要条件.判读正确的是( )
”的充要条件.判读正确的是( )A. ①②都是真命题 B. ①是真命题,②是假命题
C. ①是假命题,②是真命题 D. ①②都是假命题
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
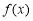 是二次函数,不等式
是二次函数,不等式 的解集为
的解集为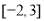 ,且
,且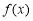 在区间
在区间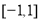 上的最小值是4.
上的最小值是4.(1)求
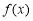 的解析式;
的解析式;(2)求
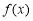 在
在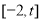 上的最大值
上的最大值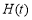 、最小值
、最小值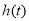 的解析式;
的解析式;(3)设
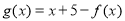 ,若对任意
,若对任意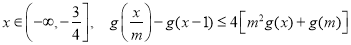 均成立,求实数
均成立,求实数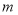 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有
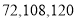 人,现采用分层抽样的方法,从该单位上述员工中抽取
人,现采用分层抽样的方法,从该单位上述员工中抽取 人调查专项附加扣除的享受情况.
人调查专项附加扣除的享受情况.(Ⅰ)应从老、中、青员工中分别抽取多少人?
(Ⅱ)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为
 .享受情况如右表,其中“
.享受情况如右表,其中“ ”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.员工
项目
A
B
C
D
E
F
子女教育
○
○
×
○
×
○
继续教育
×
×
○
×
○
○
大病医疗
×
×
×
○
×
×
住房贷款利息
○
○
×
×
○
○
住房租金
×
×
○
×
×
×
赡养老人
○
○
×
×
×
○
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设
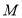 为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件
为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件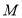 发生的概率.
发生的概率.
相关试题

