【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为3 ![]() ,b﹣c=2,cosA=﹣
,b﹣c=2,cosA=﹣ ![]() .
.
(1)求a和sinC的值;
(2)求cos(2A+ ![]() )的值.
)的值.
参考答案:
【答案】
(1)解:在三角形ABC中,由cosA=﹣ ![]() ,可得sinA=
,可得sinA= ![]() ,△ABC的面积为3
,△ABC的面积为3 ![]() ,可得:
,可得: ![]() ,
,
可得bc=24,又b﹣c=2,解得b=6,c=4,由a2=b2+c2﹣2bccosA,可得a=8,
![]() ,解得sinC=
,解得sinC= ![]() ;
;
(2)解:cos(2A+ ![]() )=cos2Acos
)=cos2Acos ![]() ﹣sin2Asin
﹣sin2Asin ![]() =
= ![]() =
= ![]()
【解析】(1)通过三角形的面积以及已知条件求出b,c,利用正弦定理求解sinC的值;(2)利用两角和的余弦函数化简cos(2A+ ![]() ),然后直接求解即可.
),然后直接求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(
=( 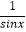 ,
, 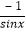 ),
), 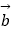 =(2,cos2x﹣sin2x).
=(2,cos2x﹣sin2x).
(1)试判断 与
与 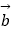 能否平行?请说明理由.
能否平行?请说明理由.
(2)若x∈(0, ],求函数f(x)=
],求函数f(x)= 
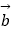 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的顶点坐标分别为A(0,1),B(2,0),C(3,2).
(1)求CD边所在直线的方程;
(2)求以AC为直径的圆M的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC1是正方体ABCD﹣A1B1C1D1的对角线.
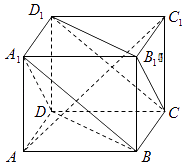
(1)求证:平面A1BD∥平面CD1B1;
(2)求证:直线AC1⊥直线BD. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}与{bn},若a1=3且对任意正整数n满足an+1﹣an=2,数列{bn}的前n项和Sn=n2+an .
(1)求数列{an},{bn}的通项公式;
(2)求数列{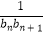 }的前n项和Tn .
}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2+y2﹣2x﹣4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y﹣4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
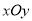 中,直线
中,直线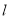 的参数方程为
的参数方程为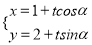 (
(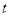 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系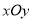 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以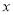 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆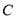 的方程为
的方程为 .
.(1)求圆
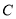 的直角坐标方程;
的直角坐标方程;(2)设圆
 与直线
与直线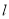 交于点
交于点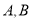 ,若点
,若点 的坐标为
的坐标为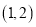 ,求
,求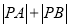 的最小值.
的最小值.
相关试题

