【题目】如图所示,一块形状为四棱柱的木料, ![]() 分别为
分别为![]() 的中点.
的中点.
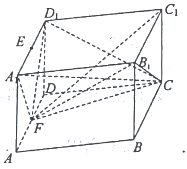
(1)要经过![]() 和
和![]() 将木料锯开,在木料上底面
将木料锯开,在木料上底面![]() 内应怎样画线?请说明理由;
内应怎样画线?请说明理由;
(2)若底面![]() 是边长为2的菱形,
是边长为2的菱形, ![]() ,
, ![]() 平面
平面![]() ,且
,且![]() ,求几何体
,求几何体![]() 的体积.
的体积.
参考答案:
【答案】(1)见解析(2)3
【解析】试题分析:(1)根据面面平行的性质,两个平行平面,被第三个平面所截,截得的交线互相平行,故得到![]() 就是应画的线;(2)几何体
就是应画的线;(2)几何体![]() 是由三棱锥
是由三棱锥![]() 和四棱锥
和四棱锥![]() 组成,分割成两个棱锥求体积即可。
组成,分割成两个棱锥求体积即可。
解析:
(1)连接![]() ,则
,则![]() 就是应画的线;
就是应画的线;
事实上,连接![]() ,在四棱柱
,在四棱柱![]() 中,
中,
因为![]() 分别为
分别为![]() 的中点,
的中点,
所以![]() ,
, ![]() ,
,
所以![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又在![]() 四棱柱中
四棱柱中![]() ,
,
所以![]() ,
,
所以点![]() 共面,
共面,
又![]() 面
面![]() ,所以
,所以![]() 就是应画线.
就是应画线.
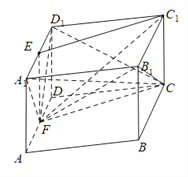
(2)几何体![]() 是由三棱锥
是由三棱锥![]() 和四棱锥
和四棱锥![]() 组成.
组成.
因为底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,
, ![]() 平面
平面![]() ,
,
连接![]() ,
, ![]() 即为三棱锥
即为三棱锥![]() 的高,
的高,
又![]() ,所以
,所以![]() ,
,
连接![]() ,
, ![]() 为四棱锥
为四棱锥![]() 的高,
的高,
又![]() ,所以
,所以![]() ,
,
所以几何体![]() 的体积为
的体积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设F1 , F2分别是C:
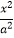 +
+ 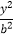 =1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
=1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为 ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
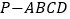 的底面
的底面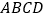 是菱形,
是菱形,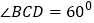 ,
,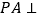 平面
平面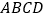 ,
, 是
是 的中点.
的中点.
(1)求证:平面
 平面
平面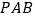 ;
;(2)棱
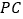 上是否存在一点
上是否存在一点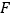 ,使得
,使得 平面
平面 ?若存在,确定
?若存在,确定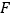 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别为CC1和BB1的中点,则异面直线AE与D1F所成角的余弦值为( )

A.0
B.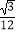
C.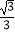
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市郊区有一加油站,2018年初汽油的存储量为50吨,计划从年初起每周初均购进汽油
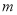 吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前
吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前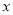 个周需求量
个周需求量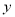 吨与
吨与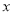 的函数关系式为
的函数关系式为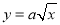
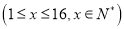 ,
, 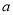 为常数,且前4个周城区内汽车的汽油需求量为100吨.
为常数,且前4个周城区内汽车的汽油需求量为100吨.(1)试写出第
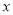 个周结束时,汽油存储量
个周结束时,汽油存储量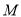 (吨)与
(吨)与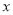 的函数关系式;
的函数关系式;(2)要使16个周内每周按计划购进汽油之后,加油站总能满足城区内和城外的需求,且每周结束时加油站的汽油存储量不超过150吨,试确定
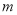 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
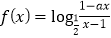 为奇函数,
为奇函数,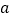 为实常数.
为实常数.(1)求
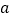 的值;
的值;(2)证明:
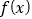 在区间
在区间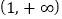 内单调递增;
内单调递增;(3)若对于区间
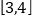 上的每一个
上的每一个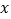 的值,不等式
的值,不等式 恒成立,求实数
恒成立,求实数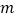 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆
 =1交于抛物线右侧的点B,F为抛物线的焦点,则|AF|+|BF|+|AB|的最大值为( )
=1交于抛物线右侧的点B,F为抛物线的焦点,则|AF|+|BF|+|AB|的最大值为( )
A.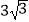
B.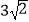
C.2
D.
相关试题

