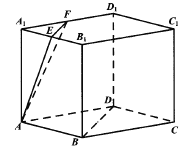
【题目】底面为菱形的直棱柱![]()
中, ![]()
分别为棱![]()
的中点.
(1)在图中作一个平面![]()
,使得![]()
,且平面![]()
.(不必给出证明过程,只要求作出![]()
与直棱柱![]()
的截面).
(2)若![]()
,求平面![]()
与平面![]()
的距离![]()
.
参考答案:
【答案】(1)见解析;(2)![]()
.
【解析】试题分析:(1)作面面平行,实质作线线平行,而线线平行的寻找往往利用平几知识,如三角形中位线、平行四边形性质等,本题中已有![]()
,根据对称性在平面![]()
中寻找另一组平行线,(2)利用向量投影可求两平面之间距离,先根据条件建立恰当直角坐标系,设立各点坐标,解方程组得平面![]()
的法向量![]()
,利用向量数量积求向量![]()
在![]()
方向上投影的绝对值,即为平面![]()
与平面![]()
的距离![]()
.
试题解析:
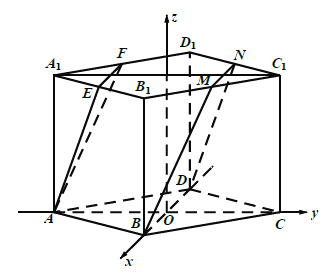
(1)如图,取![]()
的中点![]()
,连接![]()
,则平面![]()
即为所求平面![]()
.
(2)如图,连接![]()
交![]()
于![]()
,
∵在直棱柱![]()
中,底面为菱形,
∴![]()
,
∴分别以![]()
为![]()
轴, ![]()
为原点建立如图所示空间直角坐标系,
又∵所有棱长为2, ![]()
,
∴![]()
, ![]()
, ![]()
,
∴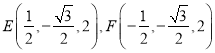
,
∴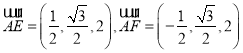
, ![]()
,
设![]()
是平面![]()
的一个法向量,则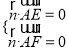
,即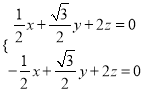
,
令![]()
得![]()
, ![]()
,
∴点![]()
到平面![]()
的距离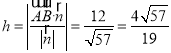
,
∴平面![]()
与平面![]()
的距离![]()
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
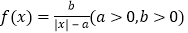 的图象形如汉字“囧”,故称其为“囧函数”.
的图象形如汉字“囧”,故称其为“囧函数”.下列命题:
①“囧函数”的值域为
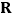 ;
;②“囧函数”在
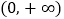 上单调递增;
上单调递增;③“囧函数”的图象关于
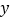 轴对称;
轴对称;④“囧函数”有两个零点;
⑤“囧函数”的图象与直线
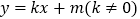 至少有一个交点.其中正确命题的个数为( )
至少有一个交点.其中正确命题的个数为( )A. 1 B. 2
C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图:
组别
锻炼次数
频数(人)
频率
1
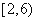
2
0.04
2
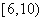
11
0.22
3

16
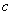
4
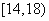
15
0.30
5



6
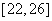
2
0.04
[
合计

1.00

(1)求频率分布表中
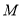 、
、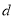 、
、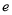 及频率分布直方图中
及频率分布直方图中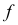 的值;
的值;(2)求参加锻炼次数的众数(直接写出答案,不要求计算过程);
(3)若参加锻炼次数不少于18次为及格,估计这次体育锻炼的及格率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年1月1日,作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
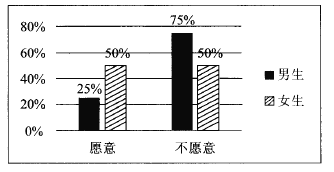
(1)根据条件完成下列
列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
愿意
不愿意
总计
男生
女生
总计
(2)水上挑战项目共有两关,主办方规定:挑战过程依次进行,每一关都有两次机会挑战,通过第一关后才有资格参与第二关的挑战,若甲参加每一关的每一次挑战通过的概率均为
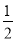
,记甲通过的关数为
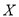
,求

的分布列和数学期望.
参考公式与数据:
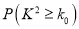
0.1
0.05
0.025
0.01
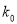
2.706
3.841
5.024
6.635
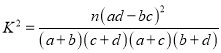
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·重庆高二检测)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
 AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.
(1)证明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知曲线
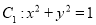 ,将曲线
,将曲线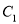 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的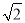 倍和
倍和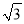 倍后,得到曲线
倍后,得到曲线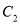
(1)试写出曲线
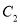 的参数方程;
的参数方程;(2)在曲线
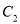 上求点
上求点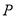 ,使得点
,使得点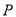 到直线
到直线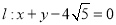 的距离最大,并求距离最大值.
的距离最大,并求距离最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
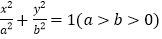 经过点
经过点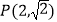 ,离心率
,离心率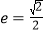 ,直线
,直线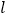 的方程为
的方程为 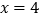 .
.(1)求椭圆
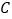 的方程;
的方程; (2)经过椭圆右焦点
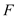 的任一直线(不经过点
的任一直线(不经过点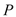 )与椭圆交于两点
)与椭圆交于两点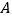 ,
,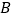 ,设直线
,设直线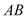 与
与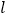 相交于点
相交于点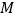 ,记
,记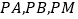 的斜率分别为
的斜率分别为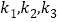 ,问:
,问: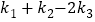 是否为定值,若是,求出此定值,若不是,请说明理由.
是否为定值,若是,求出此定值,若不是,请说明理由.
相关试题

