【题目】设 A(x1 , y1),B(x2 , y2)是函数f(x)=x﹣ ![]() 的图象上任意两点,若 M为 A,B的中点,且 M的横坐标为1.
的图象上任意两点,若 M为 A,B的中点,且 M的横坐标为1.
(1)求y1+y2;
(2)若Tn= ![]() ,n∈N* , 求 Tn;
,n∈N* , 求 Tn;
(3)已知数列{an}的通项公式an= ![]() (n≥1,n∈N*),数列{an}的前n项和为Sn , 若不等式2nSn<m2n﹣4Tn+5对任意n∈N*恒成立,求m的取值范围.
(n≥1,n∈N*),数列{an}的前n项和为Sn , 若不等式2nSn<m2n﹣4Tn+5对任意n∈N*恒成立,求m的取值范围.
参考答案:
【答案】
(1)解:由已知点M为线段AB的中点,则:x1+x2=2,
∴ ![]()
(2)解:由(1),当x1+x2=2时,有f(x1)+f(x2)=2,
故 ![]()
由Tn= ![]() ,
,
Tn= ![]() ,
,
2Tn= ![]() =
= ![]() ×2n×2=2n,
×2n×2=2n,
∴Tn=n
(3)解:由已知:Sn=1+ ![]() ,
,
![]() =
= ![]() +…+
+…+ ![]() ,
, ![]() ,
,
∴Sn=3﹣ ![]() .
.
不等式2nSn<m2n﹣4Tn+5即32n﹣(n+3)<m2n﹣4n+5,
也即(m﹣3)2n>3n﹣8,即m﹣3> ![]() 恒成立,
恒成立,
故只需 ![]() .
.
令bn= ![]() ,
,
当n≥2时,bn﹣bn﹣1= ![]() ,
,
当n≤4时,bn﹣bn﹣1>0,当n≥5时,bn﹣bn﹣1<0,
故b1<b2<b3<b4; b4>b5>b6>
故(bn)max=b4= ![]() ,
,
∴m﹣3> ![]() ,解得:m>
,解得:m> ![]()
【解析】(1)利用中点坐标公式即可得出;(2)由(1),当x1+x2=2时,有f(x1)+f(x2)=2,利用此结论可得Tn . (3)利用“错位相减法”、等比数列的前n项和公式即可得出Sn . 不等式2nSn<m2n﹣4Tn+5,即m﹣3> ![]() 恒成立,故只需
恒成立,故只需 ![]() .令bn=
.令bn= ![]() ,研究其单调性即可得出.
,研究其单调性即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系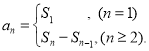 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:x2+4y2=16,点M(2,1).
(1)求椭圆C的焦点坐标和离心率;
(2)求通过M点且被这点平分的弦所在的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】雾霾天气是一种大气污染状态,PM2.5被认为是造成雾霾天气的“元凶”,PM2.5日均值越小,空气质量越好.国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如表:
PM2.5日均值
(微克/立方米)0﹣﹣35
35﹣﹣75
75﹣﹣115
115﹣﹣150
150﹣﹣250
250以上
空气质量等级
1级
优2级
良3级
轻度污染4级
中度污染5级
重度污染6级
严重污染由某市城市环境监测网获得4月份某5天甲、乙两城市的空气质量指数数据,用茎叶图表示,如图所示.
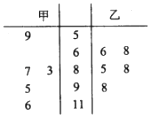
(1)试根据统计数据,分别写出两城区的PM2.5日均值的中位数,并从中位数角度判断哪个城区的空气质量较好?
(2)考虑用频率估计概率的方法,试根据统计数据,估计甲城区某一天空气质量等级为3
(3)分别从甲、乙两个城区的统计数据中任取一个,试求这两城区空气质量等级相同的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接中国共产党的十九大的到来,某校举办了“祖国,你好”的诗歌朗诵比赛.该校高三年级准备从包括甲、乙、丙在内的7名学生中选派4名学生参加,要求甲、乙、丙这3名同学中至少有1人参加,且当这3名同学都参加时,甲和乙的朗诵顺序不能相邻,那么选派的4名学生不同的朗诵顺序的种数为( )
A. 720 B. 768 C. 810 D. 816
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知D是以点A(4,1),B(﹣1,﹣6),C(﹣2,3)为顶点的三角形区域(包括边界及内部).
(1)写出表示区域D的不等式组;
(2)设点B(﹣1,﹣6)、C(﹣2,3)在直线4x﹣3y﹣a=0的异侧,求a的取值范围;
(3)若目标函数z=kx+y(k<0)的最小值为﹣k﹣6,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x>0,y>0,且2x+8y﹣xy=0,求:
(1)xy的最小值;
(2)x+y的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子装有六张卡片,上面分别写着如下六个函数:
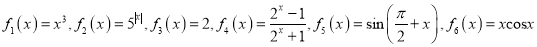 .
.(I)判断这
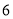 个函数的奇偶性;
个函数的奇偶性;(II)从中任意拿取两张卡片,若其中至少有一张卡片上写着的函数为奇函数.在此条件下,求两张卡片上写着的函数相加得到的新函数为奇函数的概率.
相关试题

