【题目】某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算该项目月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似地表示为:
(吨)之间的函数关系可以近似地表示为: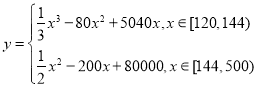 ,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为
,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为![]() 元,若该项目不获利,政府将给予补贴.
元,若该项目不获利,政府将给予补贴.
(1)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
参考答案:
【答案】(1)不能获利,政府每月至少补贴![]() 元;(2)每月处理量为
元;(2)每月处理量为![]() 吨时,平均成本最低.
吨时,平均成本最低.
【解析】
(1)利用:(生物的柴油总价值)![]() (对应段的月处理成本)
(对应段的月处理成本)![]() 利润,根据利润的正负以及大小来判断是否需要补贴,以及补贴多少;(2)考虑:(月处理成本)
利润,根据利润的正负以及大小来判断是否需要补贴,以及补贴多少;(2)考虑:(月处理成本)![]() (月处理量)
(月处理量)![]() 每吨的平均处理成本,即为
每吨的平均处理成本,即为![]() ,计算
,计算![]() 的最小值,注意分段.
的最小值,注意分段.
(1)当![]() 时,该项目获利为
时,该项目获利为![]() ,则
,则![]()
∴当![]() 时,
时,![]() ,因此,该项目不会获利
,因此,该项目不会获利
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
所以政府每月至少需要补贴![]() 元才能使该项目不亏损;
元才能使该项目不亏损;
(2)由题意可知,生活垃圾每吨的平均处理成本为: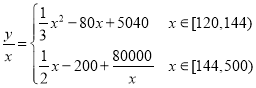
当![]() 时,
时,![]()
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() ;
;
当![]() 时,
时,![]()
当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最小值
取得最小值![]()
因为![]() ,所以当每月处理量为
,所以当每月处理量为![]() 吨时,才能使每吨的平均处理成本最低.
吨时,才能使每吨的平均处理成本最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对某种书籍每册的成本费
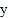 (元)与印刷册数
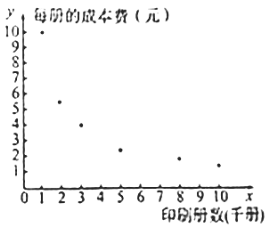
(元)与印刷册数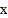 (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.


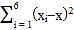
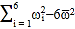
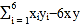

4.83
4.22
0.3775
60.17
0.60
-39.38
4.8
其中
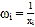 ,
,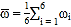 .
.为了预测印刷
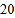 千册时每册的成本费,建立了两个回归模型:
千册时每册的成本费,建立了两个回归模型: ,
,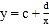 .
.(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求
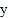 关于
关于 的回归方程,并预测印刷
的回归方程,并预测印刷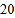 千册时每册的成本费.
千册时每册的成本费.附:对于一组数据
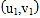 ,
,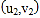 ,…,
,…,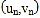 ,其回归方程
,其回归方程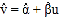 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: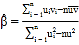 ,
,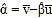 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=2x﹣cosx,{an}是公差为
 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则  =( )
=( )
A.0
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
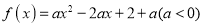 ,若
,若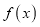 在区间[2,3]上有最大值1.
在区间[2,3]上有最大值1.(1)求
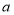 的值;
的值;(2)求函数
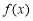 在区间
在区间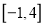 上的值域;
上的值域;(3)若
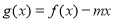 在[2,4]上单调,求实数
在[2,4]上单调,求实数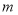 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
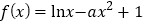 .
.(1)讨论
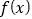 的单调性;
的单调性;(2)若
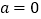 ,
,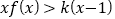 在
在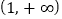 上恒成立,求整数
上恒成立,求整数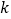 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小金同学在学校中贯彻着“边玩边学”的学风,他在“汉诺塔”的游戏中发现了数列递推的奥妙:有
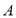 、
、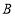 、
、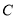 三个木桩,
三个木桩,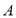 木桩上套有编号分别为
木桩上套有编号分别为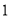 、
、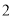 、
、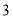 、
、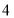 、
、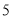 、
、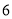 、
、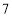 的七个圆环,规定每次只能将一个圆环从一个木桩移动到另一个木桩,且任意一个木桩上不能出现“编号较大的圆环在编号较小的圆环之上”的情况,现要将这七个圆环全部套到
的七个圆环,规定每次只能将一个圆环从一个木桩移动到另一个木桩,且任意一个木桩上不能出现“编号较大的圆环在编号较小的圆环之上”的情况,现要将这七个圆环全部套到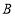 木桩上,则所需的最少次数为( )
木桩上,则所需的最少次数为( )
A.
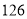 B.
B. 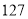 C.
C. 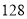 D.
D. 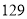
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市国庆节
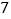 天假期的楼房认购量(单位:套)与成交量(单位:套)的折线图如图所示,小明同学根据折线图对这
天假期的楼房认购量(单位:套)与成交量(单位:套)的折线图如图所示,小明同学根据折线图对这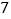 天的认购量与成交量作出如下判断:①日成交量的中位数是
天的认购量与成交量作出如下判断:①日成交量的中位数是 ;②日成交量超过日平均成交量的有
;②日成交量超过日平均成交量的有 天;③认购量与日期正相关;④
天;③认购量与日期正相关;④ 月
月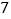 日认购量的增量大于
日认购量的增量大于 月
月 日成交量的增量.上述判断中错误的个数为( )
日成交量的增量.上述判断中错误的个数为( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

