【题目】如图所示,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为
=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为 ![]() .
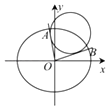
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点M(x0 , y0)是椭圆C上的动点,过原点O引两条射线l1 , l2与圆M:(x﹣x0)2+(y﹣y0)2= ![]() 分别相切,且l1 , l2的斜率k1 , k2存在.
分别相切,且l1 , l2的斜率k1 , k2存在.
①试问k1k2是否定值?若是,求出该定值,若不是,说明理由;
②若射线l1 , l2与椭圆C分别交于点A,B,求|OA||OB|的最大值.
参考答案:
【答案】解:(Ⅰ)由2c=2,c=1,设直线直线y=x被与椭圆C相交于P,Q两点,
则丨OP丨= ![]() ,设P(
,设P( ![]() ,
, ![]() ),代入椭圆方程,
),代入椭圆方程, ![]() ,①
,①
由a2﹣b2=1,②
解得:a2=2,b2=1,
∴椭圆的标准方程: ![]() ;
;
(Ⅱ)①设射线l的方程y=kx,A(x1 , y1),B(x2 , y2),
由 ![]() =
= ![]() ,两边平方得(3x02﹣2)k2﹣6x0y0k+3y02﹣2=0,
,两边平方得(3x02﹣2)k2﹣6x0y0k+3y02﹣2=0,
由y02=1﹣ ![]() ,
,
∴k1k2= ![]() =
= 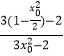 =﹣
=﹣ ![]() ,
,
∴k1k2为定值,定值﹣ ![]() ,
,
②方法一:联立 ![]() ,消去y,x12=
,消去y,x12= ![]() ,丨OA丨=
,丨OA丨= ![]() ,同理丨OA丨=
,同理丨OA丨= ![]() ,
,
|OA|2|OB|2= ![]()
![]() =4×
=4× ![]() =
= ![]() =2+
=2+ ![]() ,
,
=2+ 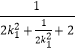 ≤
≤ ![]() ,当且仅当k12=
,当且仅当k12= ![]() ,取等号,
,取等号,
∴|OA||OB|的最大值为 ![]() ,
,
方法二:联立 ![]() ,消去y,x12=
,消去y,x12= ![]() ,丨OA丨=
,丨OA丨= ![]() ,同理丨OA丨=
,同理丨OA丨= ![]() ,
,
则|OA|2+|OB|2= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() =3,
=3,
由|OA|2+|OB|2≥2|OA||OB|,则|OA||OB|≤ ![]() ,当且仅当|OA|=|OB|时,取等号,
,当且仅当|OA|=|OB|时,取等号,
∴|OA||OB|的最大值 ![]() .
.
【解析】(Ⅰ)由c=2,求得P点坐标,代入椭圆方程,由a2﹣b2=1,即可求得a和b的值,即可求得椭圆方程;(Ⅱ)①设射线l的方程y=kx,代入椭圆方程,由韦达定理即可求得k1k2= ![]() ,由y02=1﹣
,由y02=1﹣ ![]() ,即可求得k1k2=﹣
,即可求得k1k2=﹣ ![]() ;②方法一:分别求得直线OA及OB的方程代入椭圆方程,求得|OA|及|OB|,利用基本不等式的性质,即可求得|OA||OB|的最大值;
;②方法一:分别求得直线OA及OB的方程代入椭圆方程,求得|OA|及|OB|,利用基本不等式的性质,即可求得|OA||OB|的最大值;
方法二:|OA|2+|OB|2= ![]() +
+ ![]() ,y02=1﹣
,y02=1﹣ ![]() ,代入即可求得:|OA|2+|OB|2=3,由|OA|2+|OB|2≥2|OA||OB|,即可求得|OA||OB|的最大值.
,代入即可求得:|OA|2+|OB|2=3,由|OA|2+|OB|2≥2|OA||OB|,即可求得|OA||OB|的最大值.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,等腰梯形ABCD的底角A等于60°.直角梯形ADEF所在的平面垂直于平面 ABCD,∠EDA=90°,且ED=AD=2AF=2AB=2.
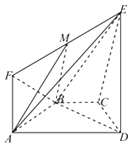
(Ⅰ)证明:平面ABE⊥平面EBD;
(Ⅱ)点M在线段EF上,试确定点M的位置,使平面MAB与平面ECD所成的角的余弦值为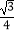 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】有人用三段论进行推理:“函数
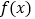 的导函数
的导函数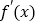 的零点即为函数
的零点即为函数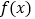 的极值点,函数
的极值点,函数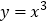 的导函数的零点为
的导函数的零点为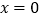 ,所以
,所以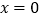 是函数
是函数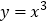 的极值点 ”,上面的推理错误的是( )
的极值点 ”,上面的推理错误的是( )A. 大前提 B. 小前提 C. 推理形式 D. 以上都是
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元,甲、乙电视台的广告费标准分别是500元/分钟和200元分钟,假设甲、乙两个电视台为该公司做的广告能给公司带来的收益分别为0.4万元/分钟和0.2万元分钟,那么该公司合理分配在甲、乙两个电视台的广告时间,能使公司获得最大的收益是()万元
A.72B.80C.84D.90
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,给出如下命题:
中,给出如下命题:①
 是
是 所在平面内一定点,且满足
所在平面内一定点,且满足 ,则
,则 是
是 的垂心;
的垂心;②
 是
是 所在平面内一定点,动点
所在平面内一定点,动点 满足
满足 ,
, ,则动点
,则动点 一定过
一定过 的重心;
的重心;③
 是
是 内一定点,且
内一定点,且 ,则
,则 ;
;④若
 且
且 ,则
,则 为等边三角形,
为等边三角形,其中正确的命题为_____(将所有正确命题的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某研究型学习小组调查研究高中生使用智能手机对学习的影响,部分统计数据如下:
使用智能手机
不使用智能手机
合计
学习成绩优秀
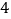
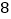
学习成绩不优秀
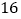
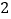
合计
(1)根据以上统计数据,你是否有
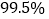 的把握认为使用智能手机对学习有影响?
的把握认为使用智能手机对学习有影响?(2)为了进一步了解学生对智能手机的使用习惯,现在对以上使用智能手机的高中时采用分层抽样的方式,抽取一个容量为
 的样本,若抽到的学生中成绩不优秀的比成绩优秀的多
的样本,若抽到的学生中成绩不优秀的比成绩优秀的多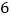 人,求
人,求 的值.
的值.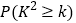
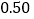
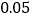


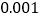
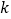


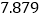
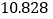

-
科目: 来源: 题型:
查看答案和解析>>【题目】求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ;
(2)与直线2x + y + 5 = 0垂直;
相关试题

