【题目】已知![]() 是定义域为
是定义域为![]() 的奇函数,且
的奇函数,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)证明![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(3)求不等式![]() 的解集.
的解集.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)由![]() 是定义域为
是定义域为![]() 的奇函数可得
的奇函数可得![]() ,再由
,再由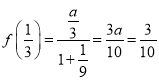 ,解得
,解得![]() ,可求函数
,可求函数![]() 的解析式;(2)任取
的解析式;(2)任取![]() ,将
,将![]() 分解因式,可证明
分解因式,可证明![]() ,从而可得结论;(3)根据
,从而可得结论;(3)根据![]() 在区间
在区间![]() 上是增函数,结合函数的定义域列不等式组求解即可.
上是增函数,结合函数的定义域列不等式组求解即可.
试题解析:(1)由题意可得![]() ,∴
,∴![]() ,
,
∴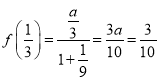 ,解得
,解得![]() ,∴
,∴![]() .
.
(2)设![]() ,则
,则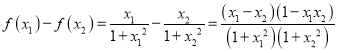 ,
,
∵![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() 在
在![]() 上是增函数.
上是增函数.
(3)由![]() 得
得![]() ,即
,即![]() ,
,
由已知及(2)可得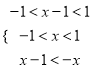 ,解得
,解得![]() ,
,
∴原不等式的解集为![]() .
.
【方法点晴】本题主要考查抽象函数的定义域、函数的单调性及利用单调性函数解不等式,属于难题. 利用单调性函数解不等式应注意以下三点:(1)一定注意函数的定义域(这一点是同学们容易疏忽的地方,不能掉以轻心);(2)注意应用函数的奇偶性(往往需要先证明是奇函数还是偶函数);(3)化成![]() 后再利用单调性和定义域列不等式组..
后再利用单调性和定义域列不等式组..
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,已知
中,已知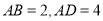 ,点
,点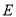 、
、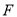 分别在
分别在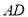 、
、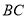 上,且
上,且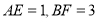 ,将四边形
,将四边形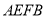 沿
沿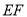 折起,使点
折起,使点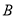 在平面
在平面 上的射影
上的射影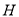 在直线
在直线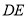 上.
上.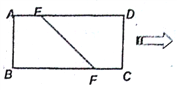
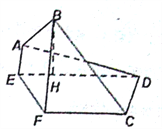
(I)求证:
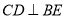 ;
;(II)求点
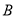 到平面
到平面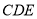 的距离;
的距离;(III)求直线
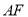 与平面
与平面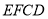 所成的正弦值.
所成的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2+log3x,x∈[1,9],求y=[f(x)]2+f(x2)的最大值,及y取最大值时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若曲线
 在
在 处的切线方程为
处的切线方程为 ,求
,求 的单调区间;
的单调区间;(2)若
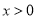 时,
时,  恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
相关试题

