【题目】如图,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,将四边形
,将四边形![]() 沿
沿![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直线
在直线![]() 上.
上.
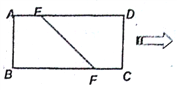
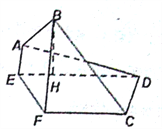
(I)求证: ![]() ;
;
(II)求点![]() 到平面
到平面![]() 的距离;
的距离;
(III)求直线![]() 与平面
与平面![]() 所成的正弦值.
所成的正弦值.
参考答案:
【答案】(1)见解析(2)2(3)![]()
【解析】试题分析:
(1)由折叠关系可得![]() 平面
平面![]() ,
, ![]() .
.
(2)利于题意结合勾股定理列方程组,求解可得点![]() 到平面
到平面![]() 的距离为2;
的距离为2;
(3)做出直线与平面所成的角,结合(1)(2)的结论可得直线![]() 与平面
与平面![]() 所成的正弦值为
所成的正弦值为![]() .
.
试题解析:
解:(1)由于![]() 平面
平面![]() ,
, ![]() ,又由于
,又由于![]() ,
, ![]() ,
,
![]() 平面
平面![]() ,
, ![]() .
.
法一:(2)设![]() ,
, ![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 于
于![]() ,
,
因线段![]() ,
, ![]() 在翻折过程中长度不变,根据勾股定理:
在翻折过程中长度不变,根据勾股定理:
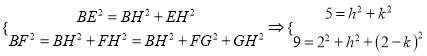 ,可解得
,可解得![]() ,
,
![]() 线段
线段![]() 长度为
长度为![]() ,即点
,即点![]() 的平面
的平面![]() 的距离为
的距离为![]() .
.
(2)延长![]() 交
交![]() 于点
于点![]() ,因为
,因为![]()
点![]() 到平面
到平面![]() 的距离为点
的距离为点![]() 到平面
到平面![]() 距离的
距离的![]() ,
,
![]() 点
点![]() 平面
平面![]() 的距离为
的距离为![]() ,而
,而![]() ,
,
直线![]() 与平面
与平面![]() 新角的正弦值为
新角的正弦值为![]() .
.
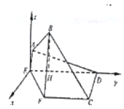
法二:(2)如图,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() 平面
平面![]() ,分别以
,分别以![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,设点
轴建立空间直角坐标系,设点![]() ,由于
,由于![]() ,
,
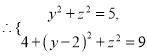 解得
解得![]() 于是
于是![]() ,所以线段
,所以线段![]() 的长度为
的长度为![]() .
.
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
(3)从而![]() ,故
,故![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,
,
则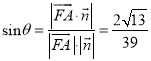
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2sin(x-
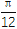 )-
)-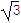 ,现将f(x)的图象向左平移
,现将f(x)的图象向左平移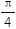 个单位长度,再向上平移
个单位长度,再向上平移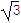 个单位长度,得到函数g(x)的图象.
个单位长度,得到函数g(x)的图象.(1)求f(
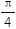 )+g(
)+g(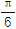 )的值;
)的值;(2)若a,b,c分别是△ABC三个内角A,B,C的对边,a+c=4,且当x=B时,g(x)取得最大值,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 sinωx·cosωx-cos2ωx(ω>0)的最小正周期为
sinωx·cosωx-cos2ωx(ω>0)的最小正周期为 .
.(1)求ω的值;
(2)在△ABC中,sinB,sinA,sinC成等比数列,求此时f(A)的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
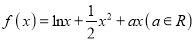 ,
, 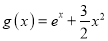 .
.(Ⅰ)讨论
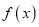 的极值点的个数;
的极值点的个数;(Ⅱ)若对于任意
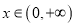 ,总有
,总有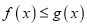 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2+log3x,x∈[1,9],求y=[f(x)]2+f(x2)的最大值,及y取最大值时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
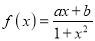 是定义域为
是定义域为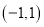 的奇函数,且
的奇函数,且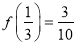 .
.(1)求
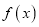 的解析式;
的解析式;(2)证明
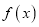 在区间
在区间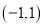 上是增函数;
上是增函数;(3)求不等式
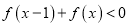 的解集.
的解集.
相关试题

