【题目】P(x0 , y0)(x0≠±a)是双曲线E: ![]() 上一点,M,N分别是双曲线E的左右顶点,直线PM,PN的斜率之积为
上一点,M,N分别是双曲线E的左右顶点,直线PM,PN的斜率之积为 ![]() .
.
(1)求双曲线的离心率;
(2)过双曲线E的右焦点且斜率为1的直线交双曲线于A,B两点,O为坐标原点,C为双曲线上一点,满足 ![]() ,求λ的值.
,求λ的值.
参考答案:
【答案】
(1)解:∵P(x0,y0)(x0≠±a)是双曲线E: ![]() 上一点,
上一点,
∴ ![]() ,①
,①
由题意又有 ![]() ,②
,②
联立①、②可得a2=5b2,c2=a2+b2,
则e= ![]() ,
,
(2)联立 ![]() ,得4x2﹣10cx+35b2=0,
,得4x2﹣10cx+35b2=0,
设A(x1,y1),B(x2,y2),
则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
设 ![]() =(x3,y3),
=(x3,y3), ![]() ,
,
即 ![]()
又C为双曲线上一点,即x32﹣5y32=5b2,
有(λx1+x2)2﹣5(λy1+y2)2=5b2,
化简得:λ2(x12﹣5y12)+(x22﹣5y22)+2λ(x1x2﹣5y1y2)=5b2,
又A(x1,y1),B(x2,y2)在双曲线上,所以x12﹣5y12=5b2,x22﹣5y22=5b2,
而x1x2﹣5y1y2=x1x2﹣5(x1﹣c)(x2﹣c)
=﹣4x1x2+5c(x1+x2)﹣5c2=﹣4 ![]() +5c
+5c ![]() ﹣5c2=
﹣5c2= ![]() ﹣35b2=
﹣35b2= ![]() 6b2﹣35b2=10b2,
6b2﹣35b2=10b2,
得λ2+4λ=0,解得λ=0或﹣4.
【解析】(1)由P点坐标满足双曲线方程,直线PM,PN的斜率之积为 ![]() 联立方程组可得a2=5b2,即可求出e的值。
联立方程组可得a2=5b2,即可求出e的值。
(2)可求出过双曲线E的右焦点且斜率为1的直线y=x-c,与双曲线联立方程组求出x1+x2,x1x2。由 ![]() 可求出
可求出![]() 值。
值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】F1、F2为椭圆的两个焦点,以F2为圆心作圆F2 , 已知圆F2经过椭圆的中心,且与椭圆相交于M点,若直线MF1恰与圆F2相切,则该椭圆的离心率e为( )
A.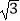 ﹣1
﹣1
B.2﹣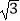
C.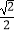
D.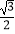
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是一位母亲给儿子作的成长记录:
年龄/周岁
3
4
5
6
7
8
9
身高/cm
94.8
104.2
108.7
117.8
124.3
130.8
139.1
根据以上样本数据,她建立了身高
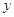 (cm)与年龄x(周岁)的线性回归方程为
(cm)与年龄x(周岁)的线性回归方程为 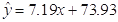 ,给出下列结论:
,给出下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本的中心点(42,117.1);
③儿子10岁时的身高是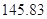 cm;
cm;
④儿子年龄增加1周岁,身高约增加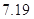 cm.
cm.
其中,正确结论的个数是
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线
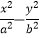 =1(a>1,b>0)的焦点距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(﹣1,0)到直线l的距离之和
=1(a>1,b>0)的焦点距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(﹣1,0)到直线l的距离之和 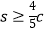 .求双曲线的离心率e的取值范围.
.求双曲线的离心率e的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
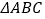 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 成等差数列
成等差数列(1)若
 ,求
,求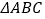 的面积
的面积(2)若
 成等比数列,试判断
成等比数列,试判断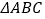 的形状
的形状
相关试题

