【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注: 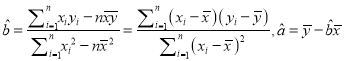 )
)
参考答案:
【答案】(1)![]() ; (2)
; (2)![]() ; (3)可靠的,理由见解析.
; (3)可靠的,理由见解析.
【解析】试题分析:(1)考查的是古典概率的计算方法.根据已知条件出其对立事件的概率概率为![]() ,则
,则![]() . (2)要求y关于x的线性回归方程
. (2)要求y关于x的线性回归方程![]() 必先求出
必先求出![]() ,
, ![]() ,所以先求出
,所以先求出![]()
![]() ,
, ![]() ,然后代入
,然后代入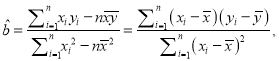 求出
求出![]() 再代入
再代入![]() 求出
求出![]() ,进而求出线性回归方程为
,进而求出线性回归方程为![]() .(3)分别将
.(3)分别将![]() 和
和![]() 代入线性回归方程这
代入线性回归方程这![]() ,所得结果分别与发芽数
,所得结果分别与发芽数![]() 和
和![]() 进行比较,相差均小于
进行比较,相差均小于![]() ,所以可以认定该线性回归方程是可靠的.
,所以可以认定该线性回归方程是可靠的.
试题解析:(1)设抽到不相邻两组数据为事件![]() ,
,
因为从第5组数据中选取2组数据共有10种情况,每种情况是等可能出现的,
其中抽到相邻两组数据的情况有4种,则![]() ,
,
所以![]() ,
,
故选取的2组数据恰好是不相邻的2天数据的概率是![]() ,
,
(2)由数据,求得![]() ,
,
![]() ,
,
![]() ,由公式得
,由公式得![]() ,
, ![]() ,
,
所以![]() 关于
关于![]() 的线性回归方程这
的线性回归方程这![]() ,
,
(3)当![]() 时,
时, ![]() ,
,
同样地,当![]() 时,
时, ![]() ,
,
所以,该研究所得到的线性回归方程是可靠.
-
科目: 来源: 题型:
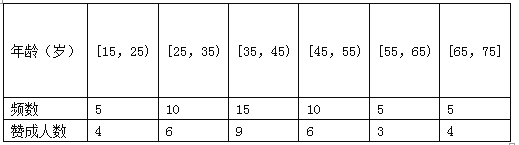
查看答案和解析>>【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;
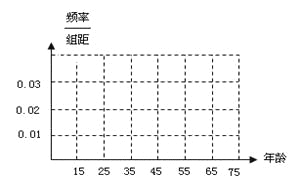
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为
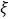 ,求随机变量
,求随机变量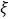 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,已知四边形
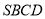 是由直角△
是由直角△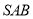 和直角梯形
和直角梯形 拼接而成的,其中
拼接而成的,其中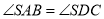
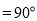 .且点
.且点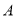 为线段
为线段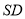 的中点,
的中点, 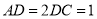 ,
, 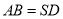 现将△
现将△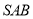 沿
沿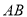 进行翻折,使得二面角
进行翻折,使得二面角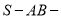
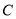 的大小为
的大小为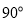 ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接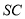 ,点
,点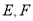 分别在线段
分别在线段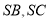 上.
上.

(1)证明:
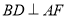 ;
;(2)若三棱锥
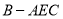 的体积为四棱锥
的体积为四棱锥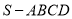 体积的
体积的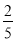 ,求点
,求点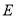 到平面
到平面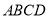 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】求和:Sn=
 +
+  +…+
+…+  ,并用数学归纳法证明.
,并用数学归纳法证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
用煤(吨)
用电(千瓦)
产值(万元)
甲产品
3
50
12
乙产品
7
20
8
但国家每天分配给该厂的煤、电有限,每天供煤至多47吨,供电至多300千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
-
科目: 来源: 题型:
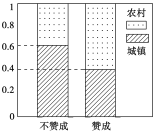
查看答案和解析>>【题目】某省高考改革实施方案指出:该省高考考生总成绩将由语文、数学、外语3门统一高考成绩和学生自主选择的学业水平等级性考试科目共同构成,该省教育厅为了解正在读高中的学生家长对高考改革方案所持的赞成态度,随机从中抽取了100名城乡家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见,如图是根据样本的调查结果绘制的等高条形图.
(1)根据已知条件与等高条形图完成下面的
 列联表,并判断我们能否有95%的把握认为“赞成高考改革方案与城乡户口有关”?
列联表,并判断我们能否有95%的把握认为“赞成高考改革方案与城乡户口有关”?
注:
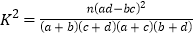 ,其中
,其中 .
.
(2)用样本的频率估计概率,若随机在全省不赞成高考改革的家长中抽取3个,记这3个家长中是城镇户口的人数为
 ,试求
,试求 的分布列及数学期望
的分布列及数学期望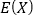 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(l)求
 的单调区间;
的单调区间;(2)若函数
 在区间
在区间 内存在唯一的极值点,求
内存在唯一的极值点,求 的值.
的值.
相关试题

