【题目】已知函数 ![]() 的定义域为R.
的定义域为R.
(Ⅰ)求实数m的范围;
(Ⅱ)若m的最大值为n,当正数a,b满足 ![]() 时,求4a+7b的最小值.
时,求4a+7b的最小值.
参考答案:
【答案】解:(Ⅰ)∵函数的定义域为R,|x+2|+|x﹣4|≥|(x+2)﹣(x﹣4)|=6,∴m≤6. (Ⅱ)由(Ⅰ)知n=6,由柯西不等式知,4a+7b= ![]() =
= ![]() ,当且仅当
,当且仅当 ![]() 时取等号,∴4a+7b的最小值为
时取等号,∴4a+7b的最小值为 ![]()
【解析】(I)利用绝对值不等式的性质即可得出.(II)利用柯西不等式的性质即可得出.
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识,掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零,以及对绝对值不等式的解法的理解,了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零,以及对绝对值不等式的解法的理解,了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
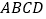 是边长为
是边长为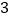 的正方形,
的正方形,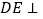 平面
平面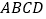 ,
,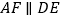 ,
,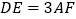 ,
,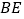 与平面
与平面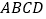 所成角为
所成角为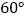 .
.(Ⅰ)求证:
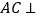 平面
平面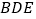 .
.(Ⅱ)求二面角
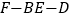 的余弦值.
的余弦值.(Ⅲ)设点
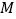 是线段
是线段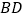 上一个动点,试确定点
上一个动点,试确定点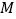 的位置,使得
的位置,使得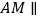 平面
平面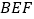 ,并证明你的结论.
,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC三个内角A,B,C所对的边分别为a,b,c,若c2sinA=5sinC,(a+c)2=16+b2 , 则△ABC的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
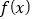 对于任意的实数
对于任意的实数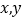 都有
都有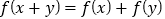 成立,且当
成立,且当 时
时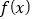 <0恒成立.
<0恒成立.(1)判断函数
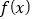 的奇偶性;
的奇偶性;(2)若
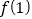 =-2,求函数
=-2,求函数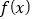 在
在 上的最大值;
上的最大值;(3)求关于
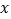 的不等式
的不等式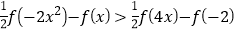 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,

(1)求图中
 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在 岁的人数;
岁的人数;(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为
 ,求
,求 的分布列及均值.
的分布列及均值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司进行仓储机器人升级换代期间,第一年有机器人
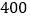 台,平均每台机器人创收利润
台,平均每台机器人创收利润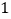 万元.预测以后每年平均每台机器人创收利润都比上一年增加
万元.预测以后每年平均每台机器人创收利润都比上一年增加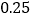 万元,但该物流公司在用机器人数量每年都比上一年减少
万元,但该物流公司在用机器人数量每年都比上一年减少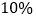 .
.(1)设第
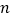 年平均每台机器人创收利润为
年平均每台机器人创收利润为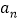 万元,在用机器人数量为
万元,在用机器人数量为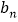 台,求
台,求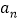 ,
,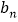 的表达式;
的表达式;(2)依上述预测,第几年该物流公司在用机器人创收的利润最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂某种产品的年固定成本为250万元,每生产
 千件,需另投入成本为
千件,需另投入成本为 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时
(万元).当年产量不小于80千件时 (万元).每件商品售价为0.05万元.通过分析,该工厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过分析,该工厂生产的商品能全部售完.(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
相关试题

