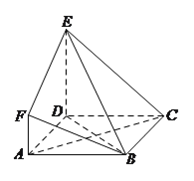
【题目】如图,![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)设点![]() 是线段
是线段![]() 上一个动点,试确定点
上一个动点,试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并证明你的结论.
,并证明你的结论.
参考答案:
【答案】(1)见解析(2)![]() (3)点
(3)点![]() 是线段
是线段![]() 靠近
靠近![]() 点的三等分点.
点的三等分点.
【解析】试题分析:(1)由正方形性质得![]() ,由
,由![]() 平面
平面![]() 得
得![]() ,再根据线面垂直判定定理得
,再根据线面垂直判定定理得![]() 平面
平面![]() (2)利用空间向量求二面角:先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,根据向量数量积求向量夹角,最后根据二面角与向量夹角关系求二面角(3)设点
(2)利用空间向量求二面角:先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,根据向量数量积求向量夹角,最后根据二面角与向量夹角关系求二面角(3)设点![]() 坐标,根据
坐标,根据![]() 平面
平面![]() 得
得![]() ,列方程解得点
,列方程解得点![]() 坐标,再确定位置
坐标,再确定位置
试题解析:(Ⅰ)证明:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() .
.
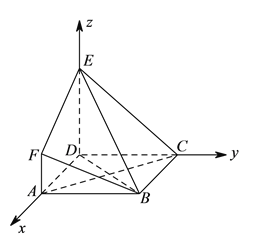
(Ⅱ)∵![]() ,
,![]() ,
,![]() 两两垂直,所以建立如图空间直角坐标系
两两垂直,所以建立如图空间直角坐标系![]() ,
,
∵![]() 与平面
与平面![]() 所成角为
所成角为![]() ,即
,即![]() ,
,
∴![]() ,
,
由![]() ,可知:
,可知:![]() ,
,![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
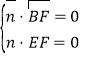 ,即
,即![]() ,
,
令![]() ,则
,则![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的法向量,
的法向量,
∴![]() ,
,
所以![]() .
.
因为二面角为锐角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.
(Ⅲ)依题意得,设![]() ,
,
则![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
此时![]() ,
,
∴点![]() 是线段
是线段![]() 靠近
靠近![]() 点的三等分点.
点的三等分点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l经过两直线l1:2x-y+4=0与l2:x-y+5=0的交点,且与直线x-2y-6=0垂直.
(1)求直线l的方程.
(2)若点P(a,1)到直线l的距离为
 ,求实数a的值.
,求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】过动点P作圆:(x﹣3)2+(y﹣4)2=1的切线PQ,其中Q为切点,若|PQ|=|PO|(O为坐标原点),则|PQ|的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱锥D﹣ABC侧棱两两垂直,E为棱AD中点,平面α过点A,且α∥平面EBC,α∩平面ABC=m,α∩平面ACD=n,则m,n所成角的余弦值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC三个内角A,B,C所对的边分别为a,b,c,若c2sinA=5sinC,(a+c)2=16+b2 , 则△ABC的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 对于任意的实数
对于任意的实数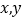 都有
都有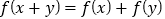 成立,且当
成立,且当 时
时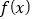 <0恒成立.
<0恒成立.(1)判断函数
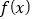 的奇偶性;
的奇偶性;(2)若
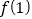 =-2,求函数
=-2,求函数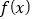 在
在 上的最大值;
上的最大值;(3)求关于
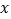 的不等式
的不等式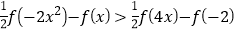 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
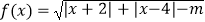 的定义域为R.
的定义域为R.
(Ⅰ)求实数m的范围;
(Ⅱ)若m的最大值为n,当正数a,b满足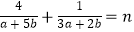 时,求4a+7b的最小值.
时,求4a+7b的最小值.
相关试题

