【题目】某工厂某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元).当年产量不小于80千件时
(万元).当年产量不小于80千件时![]() (万元).每件商品售价为0.05万元.通过分析,该工厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过分析,该工厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
参考答案:
【答案】(1)见解析;(2)100.
【解析】
分析:此题以分段函数为模型建立函数表达式,设![]() 千件产品的销售额为
千件产品的销售额为![]() 万元,当
万元,当![]() 时,年利润
时,年利润![]() ;当
;当![]() 时,年利润
时,年利润![]() .再分别求每段函数的值域得出结论。
.再分别求每段函数的值域得出结论。
详解:∵每件产品的售价为0.05万元,∴x千件产品的销售额为0.05×1 000x=50x万元.①当0<x<80时,年利润L(x)=50x-![]() x2-10x-250=-
x2-10x-250=-![]() x2+40x-250=-
x2+40x-250=-![]() (x-60)2+950,
(x-60)2+950,
∴当x=60时,L(x)取得最大值,且最大值为L(60)=950万元;
②当x≥80时,L(x)=50x-51x-![]() +1 450-250=1 200-
+1 450-250=1 200-![]() ≤1 200-2
≤1 200-2![]() =1 200-200=1 000,当且仅当x=
=1 200-200=1 000,当且仅当x=![]() ,即x=100时,L(x)取得最大值1 000万元.
,即x=100时,L(x)取得最大值1 000万元.
由于950<1 000,
∴当产量为100千件时,该工厂在这一产品的生产中所获年利润最大,最大年利润为
1 000万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
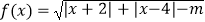 的定义域为R.
的定义域为R.
(Ⅰ)求实数m的范围;
(Ⅱ)若m的最大值为n,当正数a,b满足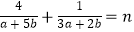 时,求4a+7b的最小值.
时,求4a+7b的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,

(1)求图中
 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在 岁的人数;
岁的人数;(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为
 ,求
,求 的分布列及均值.
的分布列及均值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司进行仓储机器人升级换代期间,第一年有机器人
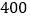 台,平均每台机器人创收利润
台,平均每台机器人创收利润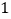 万元.预测以后每年平均每台机器人创收利润都比上一年增加
万元.预测以后每年平均每台机器人创收利润都比上一年增加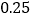 万元,但该物流公司在用机器人数量每年都比上一年减少
万元,但该物流公司在用机器人数量每年都比上一年减少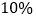 .
.(1)设第
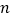 年平均每台机器人创收利润为
年平均每台机器人创收利润为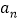 万元,在用机器人数量为
万元,在用机器人数量为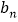 台,求
台,求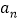 ,
,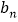 的表达式;
的表达式;(2)依上述预测,第几年该物流公司在用机器人创收的利润最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
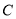 :
: 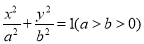 的离心率为
的离心率为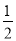 ,且过点
,且过点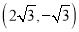 ,
,  ,
, 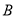 是椭圆
是椭圆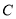 上异于长轴端点的两点.
上异于长轴端点的两点.(1)求椭圆
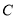 的方程;
的方程;(2)已知直线
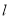 :
: 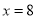 ,且
,且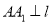 ,垂足为
,垂足为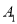 ,
, 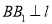 ,垂足为
,垂足为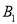 ,若
,若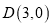 ,且
,且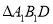 的面积是
的面积是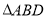 面积的5倍,求
面积的5倍,求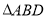 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是公比为正数的等比数列,
是公比为正数的等比数列,  .
.(1)求
 的通项公式;
的通项公式;(2)设
 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前n项和
的前n项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 过点
过点 ,直线
,直线 交
交 轴于
轴于 ,且
,且 ,
,  为坐标原点.
为坐标原点.(1)求椭圆
 的方程;
的方程;(2)设
 是椭圆
是椭圆 的上顶点,过点
的上顶点,过点 分别作直线
分别作直线 交椭圆
交椭圆 于
于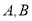 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线 过定点.
过定点.
相关试题

