【题目】方程 ![]() 在(0,2π)内有相异两解α,β,则α+β=
在(0,2π)内有相异两解α,β,则α+β=
参考答案:
【答案】![]() 或
或 ![]()
![]()
【解析】解:∵sinx+ ![]() cosx+a=0,
cosx+a=0,
∴﹣a=sinx+ ![]() cosx=2(
cosx=2( ![]() sinx+
sinx+ ![]() cosx)=2sin(x+
cosx)=2sin(x+ ![]() ),
),
令f(x)=2sin(x+ ![]() ),y=﹣a,
),y=﹣a,
∵0<x<2π,
∴ ![]() <x+
<x+ ![]() <2π+
<2π+ ![]() =
= ![]() ,
,
在同一坐标系中作出f(x)=2sin(x+ ![]() )与y=﹣a的图象,
)与y=﹣a的图象,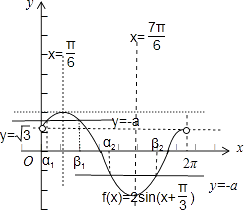
由图知,当x= ![]() ,即x+
,即x+ ![]() =
= ![]() 时,f(x)取到最大值2,当x=
时,f(x)取到最大值2,当x= ![]() 时,x+
时,x+ ![]() =
= ![]() +
+ ![]() =
= ![]() ,f(x)取到最小值﹣2;
,f(x)取到最小值﹣2;
方程sinx+ ![]() cosx+a=0在(0,2π)内有相异两解α,β直线y=﹣a与曲线f(x)=2sin(x+
cosx+a=0在(0,2π)内有相异两解α,β直线y=﹣a与曲线f(x)=2sin(x+ ![]() )在(0,2π)内有两个不同的交点,
)在(0,2π)内有两个不同的交点,
当交点的横坐标分别为α1与β1时,α1+β1= ![]() ;
;
当交点的横坐标分别为α2与β2时,α2+β2= ![]() ;
;
∴α+β= ![]() 或
或 ![]() .
.
所以答案是: ![]() 或
或 ![]() .
.
【考点精析】掌握两角和与差的正弦公式和函数的零点与方程根的关系是解答本题的根本,需要知道两角和与差的正弦公式:![]() ;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.
;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)=
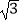 sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.
sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点. 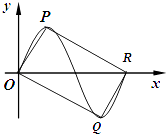
(1)求f(x)的解析式
(2)对于x∈[0,3],方程f2(x)﹣af(x)+1=0恒有四个不同的实数根,求实数a的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】汽车厂生产
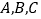 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.轿车

轿车
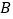
轿车
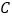
舒适型
100
150
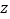
标准型
300
450
600
(1)求
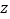 的值;
的值;(2)用分层抽样的方法在
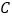 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从
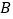 类舒适型轿车中抽取8辆,经检测它们的得分如下:
类舒适型轿车中抽取8辆,经检测它们的得分如下: . 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过
. 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过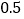 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】把函数y=sin(2x+
 )的图象向右平移
)的图象向右平移  个单位,再把所得图象上各点的横坐标缩短到原来的
个单位,再把所得图象上各点的横坐标缩短到原来的  ,则所得图象的函数解析式是( )
,则所得图象的函数解析式是( )
A.y=sin(4x+ π)
π)
B.y=sin(4x+ )
)
C.y=sin4x
D.y=sinx -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
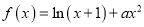 ,其中
,其中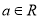
(Ⅰ)若函数
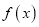 在
在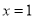 处的切线与直线
处的切线与直线 垂直,求
垂直,求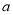 的值;
的值;(Ⅱ)讨论函数
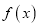 极值点的个数,并说明理由;
极值点的个数,并说明理由;(Ⅲ)若
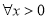 ,
, 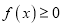 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)已知tanα=3,求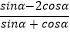 的值;
的值;
(2)已知α为第二象限角,化简cosα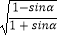 +sinα
+sinα 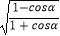 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(sinx+cosx)2+2cos2x﹣2.
(1)求函数f(x)的最小正周期和单调增区间;
(2)当x∈[ ,
, 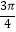 ]时,求函数f(x)的最大值,最小值.
]时,求函数f(x)的最大值,最小值.
相关试题

