【题目】汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:
类舒适型轿车中抽取8辆,经检测它们的得分如下:![]() . 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过
. 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过![]() 的概率.
的概率.
参考答案:
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆,得每个个体被抽到的概率,列出关系式,得到
类轿车10辆,得每个个体被抽到的概率,列出关系式,得到![]() 的值;(2)由题意知本题是一个古典概型,试验发生包含的事件数和满足条件的事件数,可以通过列举数出结果,根据古典概型的概率公式得到结果;(3)首先做出样本的平均数,做出试验发生包含的事件数,和满足条件的事件数,根据古典概型、型的概率公式得到结果.
的值;(2)由题意知本题是一个古典概型,试验发生包含的事件数和满足条件的事件数,可以通过列举数出结果,根据古典概型的概率公式得到结果;(3)首先做出样本的平均数,做出试验发生包含的事件数,和满足条件的事件数,根据古典概型、型的概率公式得到结果.
(1)设该厂这个月共生产轿车![]() 辆,由题意得
辆,由题意得![]() ,
,![]() .
.
(2)设所抽样中有![]() 辆舒适轿车,由题意,得
辆舒适轿车,由题意,得![]() ,因此抽取的容量为
,因此抽取的容量为![]() 的样本中,有
的样本中,有![]() 辆舒适型轿车,3辆标准型轿车.用山
辆舒适型轿车,3辆标准型轿车.用山![]() 表示2辆舒适型轿车,用
表示2辆舒适型轿车,用![]() 表示3辆标准轿车,用
表示3辆标准轿车,用![]() 表示事件“在该样本中任取2辆,其中至少有1辆,舒适轿车”,则基本事件空间包含的基本事件有:
表示事件“在该样本中任取2辆,其中至少有1辆,舒适轿车”,则基本事件空间包含的基本事件有:
![]() ,
,![]() ,故
,故![]() 个,事件
个,事件![]() 包含的基本事件有:
包含的基本事件有:
![]() ,共
,共![]() 个,故
个,故![]() ,即所求概率为
,即所求概率为![]() .
.
(3)样本平均数![]() ,设
,设![]() 表示事件“从样本中任取一数,该数与样本平均数之差的绝对不超过
表示事件“从样本中任取一数,该数与样本平均数之差的绝对不超过![]() ”,则基本事件空间中有
”,则基本事件空间中有![]() 个基本事件,事件
个基本事件,事件![]() 包括的基本事件有:
包括的基本事件有:![]() ,共
,共![]() 个,
个,![]() ,即所求概率为
,即所求概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是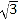 ,
, 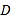 是
是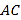 的中点.
的中点.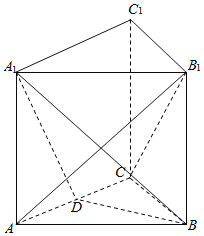
(1)求证:
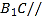 平面
平面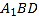 ;
;(2)求二面角
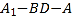 的大小;
的大小;(3)求直线
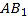 与平面
与平面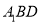 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】过椭圆
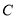 :
: 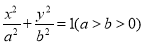 上一点
上一点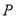 向
向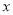 轴作垂线,垂足为右焦点
轴作垂线,垂足为右焦点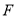 ,
,  、
、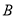 分别为椭圆
分别为椭圆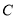 的左顶点和上顶点,且
的左顶点和上顶点,且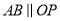 ,
, 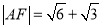 .
.(Ⅰ)求椭圆
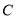 的方程;
的方程;(Ⅱ)若动直线
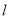 与椭圆
与椭圆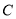 交于
交于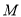 、
、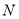 两点,且以
两点,且以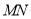 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点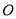 .问是否存在一个定圆与动直线
.问是否存在一个定圆与动直线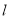 总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
总相切.若存在,求出该定圆的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)=
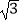 sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.
sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点. 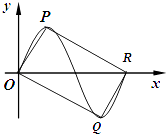
(1)求f(x)的解析式
(2)对于x∈[0,3],方程f2(x)﹣af(x)+1=0恒有四个不同的实数根,求实数a的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】把函数y=sin(2x+
 )的图象向右平移
)的图象向右平移  个单位,再把所得图象上各点的横坐标缩短到原来的
个单位,再把所得图象上各点的横坐标缩短到原来的  ,则所得图象的函数解析式是( )
,则所得图象的函数解析式是( )
A.y=sin(4x+ π)
π)
B.y=sin(4x+ )
)
C.y=sin4x
D.y=sinx -
科目: 来源: 题型:
查看答案和解析>>【题目】方程
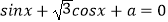 在(0,2π)内有相异两解α,β,则α+β=
在(0,2π)内有相异两解α,β,则α+β= -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
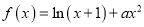 ,其中
,其中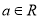
(Ⅰ)若函数
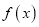 在
在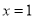 处的切线与直线
处的切线与直线 垂直,求
垂直,求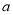 的值;
的值;(Ⅱ)讨论函数
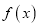 极值点的个数,并说明理由;
极值点的个数,并说明理由;(Ⅲ)若
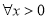 ,
, 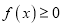 恒成立,求
恒成立,求 的取值范围.
的取值范围.
相关试题

