【题目】已知函数f(x)=(sinx+cosx)2+2cos2x﹣2.
(1)求函数f(x)的最小正周期和单调增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的最大值,最小值.
]时,求函数f(x)的最大值,最小值.
参考答案:
【答案】
(1)解:f(x)=(sinx+cosx)2+2cos2x﹣2=1+sin2x+cos2x﹣1= ![]() sin(2x+
sin(2x+ ![]() ),
),
∴f(x)的最小正周期是 ![]() =π.
=π.
令﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,解得﹣
+2kπ,解得﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,
+kπ,
∴f(x)的单调增区间是[﹣ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z.
+kπ],k∈Z.
(2)解:∵x∈[ ![]() ,
, ![]() ],∴2x+
],∴2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
∴当2x+ ![]() =
= ![]() 时,f(x)取得最大值1,
时,f(x)取得最大值1,
当2x+ ![]() =
= ![]() 时,f(x)取得最小值﹣
时,f(x)取得最小值﹣ ![]() .
.
【解析】(1)化简得f(x)=1+sin2x+cos2x﹣1= ![]() sin(2x+
sin(2x+ ![]() ),令﹣
),令﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ解得增区间;(2)根据x的范围求出2x+
+2kπ解得增区间;(2)根据x的范围求出2x+ ![]() 的范围,结合正弦函数的单调性求出f(x)的最值.
的范围,结合正弦函数的单调性求出f(x)的最值.
【考点精析】本题主要考查了三角函数的最值的相关知识点,需要掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程
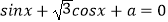 在(0,2π)内有相异两解α,β,则α+β=
在(0,2π)内有相异两解α,β,则α+β= -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
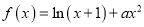 ,其中
,其中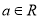
(Ⅰ)若函数
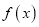 在
在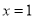 处的切线与直线
处的切线与直线 垂直,求
垂直,求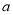 的值;
的值;(Ⅱ)讨论函数
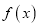 极值点的个数,并说明理由;
极值点的个数,并说明理由;(Ⅲ)若
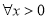 ,
, 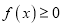 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)已知tanα=3,求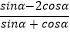 的值;
的值;
(2)已知α为第二象限角,化简cosα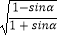 +sinα
+sinα 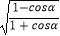 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图四棱锥
 的底面
的底面 为菱形,且
为菱形,且 ,
,  ,
,  .
.(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)二面角
 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列四个命题
①“若
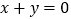 ,则互为相反数”的逆命题;
,则互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;
③“若
 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;④“不等边三角形的三个内角相等”的逆命题.
其中真命题为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分别求适合下列条件的双曲线的标准方程.
(Ⅰ)焦点在
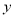 轴上,焦距是
轴上,焦距是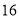 ,离心率
,离心率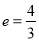 ;
;(Ⅱ)一个焦点为
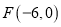 的等轴双曲线.
的等轴双曲线.
相关试题

