【题目】已知函数![]() (
(![]() ).
).
(1)当曲线![]() 在点
在点![]() 处的切线的斜率大于
处的切线的斜率大于![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若![]()
![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.(提示:
的取值范围.(提示:![]() )
)
参考答案:
【答案】(1)详见解析; (2)![]() .
.
【解析】试题分析:
(1)考查函数的定义域![]() ,且
,且![]()
![]() ,由
,由![]() ,得
,得![]() .分类讨论:
.分类讨论:
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() .
.
(2)构造新函数,令![]()
![]()
![]() ,
,![]() ,
,
则![]()
![]() ,
,![]() ,分类讨论:
,分类讨论:
①当![]() 时,可得
时,可得![]() .
.
②当![]() 时,
时,![]()
![]() .
.
综上所述,![]() .
.
试题解析:
(1)的定义域为![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.
由![]() ,得
,得![]() .当
.当![]() 时,
时,![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,
时,![]() ,
,![]() 的单调递减区间为
的单调递减区间为![]() .
.
(2)令![]()
![]()
![]() ,
,![]() ,
,
则![]()
![]()
![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减,所以当
上单调递减,所以当![]() ,
,![]() ,故只需
,故只需![]() ,即
,即![]() ,即
,即![]() ,所以
,所以![]() .
.
②当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以当![]() 时,
时,![]() 取得最大值.
取得最大值.
故只需![]() ,即
,即![]()
![]() ,
,
化简得![]()
![]() ,
,
令![]() ,得
,得![]() (
(![]() ).
).
令![]()
![]() (
(![]() ),则
),则![]()
![]() ,
,
令![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上递增,
上递增,
而![]() ,
,![]()
![]() ,所以
,所以![]() 上恒有
上恒有![]() ,
,
即当![]() 时,
时,![]()
![]() .
.
综上所述,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图
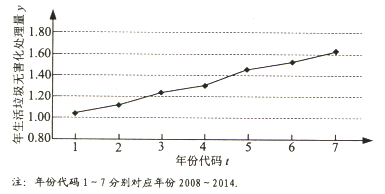
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2017年我国生活垃圾无害化处理量.
参考数据: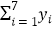 =9.32,
=9.32, 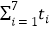 yi=40.17,
yi=40.17, 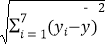 =0.55,
=0.55, 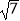 ≈2.646.
≈2.646.
参考公式:相关系数r=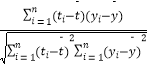 回归方程
回归方程 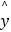 =
= 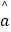 +
+ 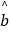 t 中斜率和截距的最小二乘估计公式分别为:
t 中斜率和截距的最小二乘估计公式分别为: 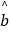 =
= 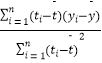 ,
, 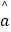 =
= 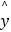 ﹣
﹣ 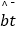 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在“一带一路”的建设中,中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料下表:

(1)在散点图中
 号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为
号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为 ,求
,求 ,并估计
,并估计 的预报值;
的预报值;(2)现准备勘探新井
 ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的 的值(
的值( 精确到0.01)相比于(1)中
精确到0.01)相比于(1)中 的值之差(即:
的值之差(即: )不超过10%,则使用位置最接近的已有旧井
)不超过10%,则使用位置最接近的已有旧井 ,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果:
,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果: ,
, )
)(3)设出油量与钻探深度的比值
 不低于20的勘探井称为优质井,在原有井号
不低于20的勘探井称为优质井,在原有井号 的井中任意勘探3口井,求恰好2口是优质井的概率.
的井中任意勘探3口井,求恰好2口是优质井的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验.为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数
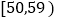
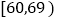



甲班频数
5
6
4
4
1
一般频数
1
3
6
5
5
(1)由以下统计数据填写下面
 列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?甲班
乙班
总计
成绩优良
成绩不优良
总计
附:
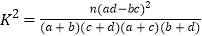 ,其中
,其中 .
.临界值表

0.10
0.05
0.025
0.010

2.706
3.841
5.024
6.635
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
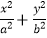 =1(a>b>0)的左右焦点F1、F2 , 离心率为
=1(a>b>0)的左右焦点F1、F2 , 离心率为  ,双曲线方程为
,双曲线方程为 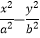 =1(a>0,b>0),直线x=2与双曲线的交点为A、B,且|AB|=
=1(a>0,b>0),直线x=2与双曲线的交点为A、B,且|AB|= 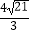 .
.
(Ⅰ)求椭圆与双曲线的方程;
(Ⅱ)过点F2的直线l与椭圆交于M、N两点,交双曲线与P、Q两点,当△F1MN(F1为椭圆的左焦点)的内切圆的面积取最大值时,求△F1PQ的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入
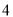 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从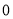 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.](1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入
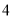 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入
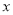 (单位:万元)
(单位:万元)1
2
3
4
5
销售收益
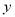 (单位:万元)
(单位:万元)2
3
2
7
由表中的数据显示,
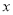 与
与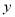 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出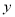 关于
关于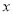 的回归直线方程.
的回归直线方程.
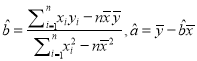
相关试题

