【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验.为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 5 | 6 | 4 | 4 | 1 |
一般频数 | 1 | 3 | 6 | 5 | 5 |
(1)由以下统计数据填写下面![]() 列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考答案:
【答案】(1)列联表见解析,在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”;(2)分布列见解析,
的前提下认为“成绩优良与教学方式有关”;(2)分布列见解析,![]() .
.
【解析】试题分析:(1)由已知数据能完成![]() 列联表,据列联表中的数据,求出
列联表,据列联表中的数据,求出![]() ,能在犯错概率不超过
,能在犯错概率不超过![]() 的前提下认为“成绩优良与教学方式有关”;(2)由题意得
的前提下认为“成绩优良与教学方式有关”;(2)由题意得![]() 的可能取值为
的可能取值为![]() ,分别求出
,分别求出![]() ,由此能求出的
,由此能求出的![]() 的分布列及数学期望.
的分布列及数学期望.
试题解析:(1)
甲班 | 乙班 | 总计 | |
成绩优良 | 9 | 16 | 25 |
成绩不优良 | 11 | 4 | 15 |
总计 | 20 | 20 | 40 |
……………2分
根据![]() 列联表中的数据,得
列联表中的数据,得![]() 的观测值为
的观测值为![]() ,
,
∴能在犯错概率不超过![]() 的前提下认为“成绩优良与教学方式有关”.………………5分
的前提下认为“成绩优良与教学方式有关”.………………5分
(2)由表可知在8人中成绩不优良的人数为![]() ,则
,则![]() 的可能取值为
的可能取值为![]() .…………6分
.…………6分
![]() ;
;![]() ;………………8分
;………………8分
![]() ;
;![]() .……………………10分
.……………………10分
∴![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
………………………11分
∴![]() .……………………12分
.……………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
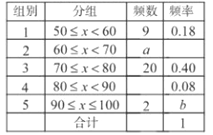

请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出
 的值;
的值;(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内?
(3)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用:列表法或树状图求出小明、小敏同时被选中的概率.(注:五位同学请用
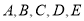 表示,其中小明为
表示,其中小明为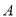 ,小敏为
,小敏为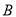 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和爸爸周末到湿地公园进行锻炼,两人上午9:00从公园入口出发,沿相同路线匀速运动,小明15分钟后到达目的地,此时爸爸离出发地的路程为1200米,小明到达目的地后立即按原路匀速返回,与爸爸相遇后,和爸爸一起从原路返回出发地.小明、爸爸在锻炼过程中离出发地的路程与小明出发的时间的函数关系如图.
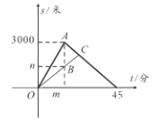
(1)图中
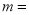 ________,
________, 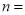 _______;
_______;(2)求小明和爸爸相遇的时刻.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
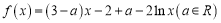 .
.(1)若函数
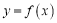 在区间
在区间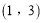 上单调,求
上单调,求 的取值范围;
的取值范围;(2)若函数
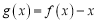 在
在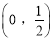 上无零点,求
上无零点,求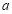 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
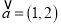 ,
, 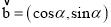 .设
.设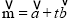 (t为实数).
(t为实数).(Ⅰ)若
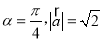 ,求当
,求当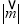 取最小值时实数t的值;
取最小值时实数t的值;(Ⅱ)若
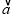 ⊥
⊥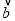 ,问:是否存在实数t,使得向量
,问:是否存在实数t,使得向量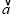 -
-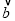 和向量
和向量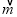 的夹角为
的夹角为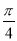 ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知右焦点为
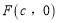 的椭圆
的椭圆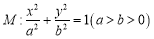 过点
过点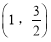 ,且椭圆
,且椭圆 关于直线
关于直线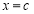 对称的图形过坐标原点.
对称的图形过坐标原点.(1)求椭圆
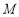 的方程;
的方程;(2)过点
 且不垂直于
且不垂直于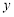 轴的直线与椭圆
轴的直线与椭圆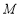 交于
交于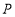 ,
,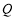 两点,点
两点,点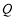 关于
关于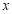 轴的对称点为
轴的对称点为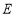 ,证明:直线
,证明:直线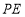 与
与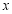 轴的交点为
轴的交点为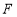 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一块圆心角为120°,半径为20cm的扇形钢片裁出一块矩形钢片,如图有两种裁法:使矩形一边在扇形的一条半径OA上,或者让矩形一边与弦AB平行,试问哪种裁法能使截得的矩形钢片面积最大?并求出这个最大值.

相关试题

