【题目】如图,在正方体![]() 中,
中,![]() 分别为
分别为![]() 的中点.
的中点.
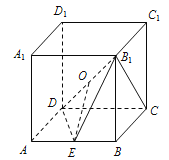
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
参考答案:
【答案】(1)详见解析,(2)详见解析
【解析】
试题(1)证明线面平行,一般利用其判定定理进行证明,即先找出线线平行,这可利用平行四边形得到:连接![]() ,设
,设![]() ,则易证四边形OEBF是平行四边形,所以
,则易证四边形OEBF是平行四边形,所以![]() ,再根据线面平行判定定理得到
,再根据线面平行判定定理得到![]() 面
面![]() .本题也可由
.本题也可由![]() 进行证明(2)证明面面垂直,一般利用线面垂直进行证明,关键是证面的垂线:因为
进行证明(2)证明面面垂直,一般利用线面垂直进行证明,关键是证面的垂线:因为![]() 面
面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() .
.
试题解析:证明(1):连接![]() ,设
,设![]() ,连接
,连接![]() , 2分
, 2分
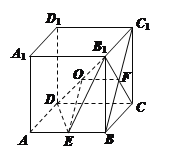
因为O,F分别是![]() 与
与![]() 的中点,所以
的中点,所以![]() ,且
,且![]() ,
,
又E为AB中点,所以![]() ,且
,且![]() ,
,
从而![]() ,即四边形OEBF是平行四边形,
,即四边形OEBF是平行四边形,
所以![]() , 6分
, 6分
又![]() 面
面![]() ,
,![]() 面
面![]() ,
,
所以![]() 面
面![]() . 8分
. 8分
(2)因为![]() 面
面![]() ,
,![]() 面
面![]() ,
,
所以![]() , 10分
, 10分
又![]() ,且
,且![]() 面
面![]() ,
,![]() ,
,
所以![]() 面
面![]() , 12分
, 12分
而![]() ,所以
,所以![]() 面
面![]() ,又
,又![]() 面
面![]() ,
,
所以面![]() 面
面![]() . 14分
. 14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 经过椭圆
经过椭圆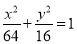 的右顶点
的右顶点 、下顶点
、下顶点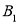 和上顶点
和上顶点 .
.(1)求圆
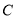 的标准方程;
的标准方程;(2)直线
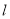 经过点
经过点 且与
且与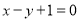 垂直,
垂直,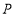 是直线
是直线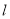 上的动点,过点
上的动点,过点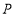 作圆
作圆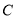 的切线,切点分别为
的切线,切点分别为 ,求四边形
,求四边形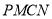 面积的最小值.
面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形
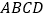 为矩形,
为矩形, 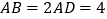 ,
,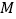 为
为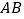 的中点,将
的中点,将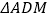 沿
沿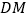 折起,得到四棱锥
折起,得到四棱锥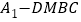 ,设
,设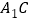 的中点为
的中点为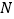 ,在翻折过程中,得到如下有三个命题:
,在翻折过程中,得到如下有三个命题:①
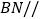 平面
平面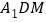 ,且
,且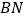 的长度为定值
的长度为定值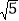 ;
;②三棱锥
 的最大体积为
的最大体积为 ;
;③在翻折过程中,存在某个位置,使得
 .
.其中正确命题的序号为__________.(写出所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高三模拟考试的学生中随机抽取
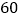 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段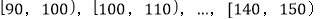 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在
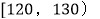 内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分;
内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分;(2)用分层抽样的方法,在分数段为
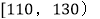 的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段
的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段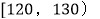 内的概率
内的概率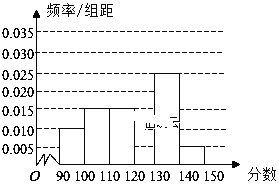
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
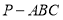 中,平面
中,平面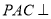 平面
平面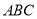 ,
,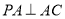 ,
,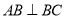 .设
.设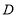 ,
,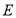 分别为
分别为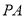 ,
,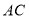 中点.
中点.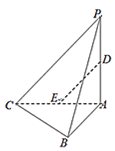
(1)求证:
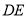
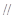 平面
平面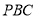 ;
;(2)求证:
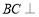 平面
平面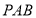 ;
;(3)试问在线段
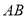 上是否存在点
上是否存在点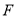 ,使得过三点
,使得过三点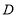 ,
,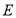 ,
,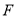 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面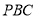 平行?若存在,指出点
平行?若存在,指出点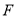 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】目前某地区有100万人,经过x年后为y万人,如果年平均增长率是1.2%,请回答下列问题:
(1)试推算出y关于x的函数关系式;
(2)计算10年后该地区的人口总数(精确到0.1万人);
(3)计算大约多少年后该地区的人口总数会达到120万(精确到1年).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在空间四边形
 中,
中, ,
,
 ,
, ,
, ,且平面
,且平面 平面
平面 .
.
(1)求证:
 ;
;(2)若直线
 与平面
与平面 所成角的余弦值为
所成角的余弦值为 ,求
,求 .
.
相关试题

