【题目】已知四边形![]() 为矩形,
为矩形, ![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,设
,设![]() 的中点为
的中点为![]() ,在翻折过程中,得到如下有三个命题:
,在翻折过程中,得到如下有三个命题:
①![]() 平面
平面![]() ,且
,且![]() 的长度为定值
的长度为定值![]() ;
;
②三棱锥![]() 的最大体积为
的最大体积为![]() ;
;
③在翻折过程中,存在某个位置,使得![]() .
.
其中正确命题的序号为__________.(写出所有正确结论的序号)
参考答案:
【答案】①②
【解析】
取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明四边形
,证明四边形![]() 为平行四边形,得出
为平行四边形,得出![]() ,可判断出命题①的正误;由
,可判断出命题①的正误;由![]() 为
为![]() 的中点,可知三棱锥
的中点,可知三棱锥![]() 的体积为三棱锥
的体积为三棱锥
![]() 的一半,并由平面
的一半,并由平面![]() 平面
平面![]() ,得出三棱锥
,得出三棱锥![]() 体积的最大值,可判断出命题②的正误;取
体积的最大值,可判断出命题②的正误;取![]() 的中点
的中点![]() ,连接
,连接![]() ,由
,由![]() ,结合
,结合![]() 得出
得出![]() 平面
平面![]() ,推出
,推出![]() 得出矛盾,可判断出命题③的正误.
得出矛盾,可判断出命题③的正误.
如下图所示:
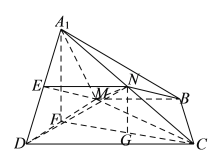
对于命题①,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
![]() ,由勾股定理得
,由勾股定理得![]() ,
,
易知![]() ,且
,且![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,所以,
的中点,所以,![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,命题①正确;
,命题①正确;
对于命题②,由![]() 为
为![]() 的中点,可知三棱锥
的中点,可知三棱锥![]() 的体积为三棱锥
的体积为三棱锥![]() 的一半,当平面
的一半,当平面![]() 平面
平面![]() 时,三棱锥
时,三棱锥![]() 体积取最大值,
体积取最大值,
取![]() 的中点
的中点![]() ,则
,则![]() ,且
,且![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 的面积为
的面积为![]() ,
,
所以,三棱锥![]() 的体积的最大值为
的体积的最大值为![]() ,
,
则三棱锥![]() 的体积的最大值为
的体积的最大值为![]() ,命题②正确;
,命题②正确;
对于命题③,![]() ,
,![]() 为
为![]() 的中点,所以,
的中点,所以,![]() ,
,
若![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
由于![]() 平面
平面![]() ,
,![]() ,事实上,易得
,事实上,易得![]() ,
,![]() ,
,
![]() ,由勾股定理可得
,由勾股定理可得![]() ,这与
,这与![]() 矛盾,命题③错误.
矛盾,命题③错误.
故答案为:①②.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
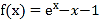 (
(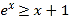 是自然对数的底数)
是自然对数的底数)(1)求证:
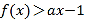
(2)若不等式
 在
在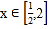 上恒成立,求正数
上恒成立,求正数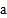 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面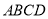 是边长为
是边长为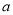 的菱形,
的菱形, 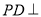 平面
平面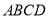 ,
, 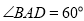 ,
, 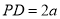 ,
, 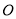 为
为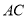 与
与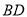 的交点,
的交点, 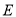 为棱
为棱 上一点.
上一点.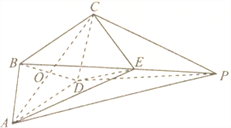
(1)证明:平面
 平面
平面 ;
;(2)若
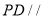 平面
平面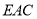 ,三棱锥
,三棱锥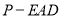 的体积为
的体积为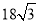 ,求
,求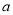 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
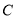 经过椭圆
经过椭圆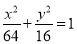 的右顶点
的右顶点 、下顶点
、下顶点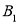 和上顶点
和上顶点 .
.(1)求圆
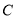 的标准方程;
的标准方程;(2)直线
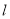 经过点
经过点 且与
且与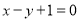 垂直,
垂直,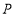 是直线
是直线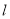 上的动点,过点
上的动点,过点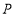 作圆
作圆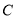 的切线,切点分别为
的切线,切点分别为 ,求四边形
,求四边形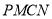 面积的最小值.
面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高三模拟考试的学生中随机抽取
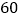 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段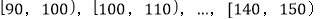 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在
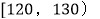 内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分;
内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分;(2)用分层抽样的方法,在分数段为
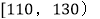 的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段
的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段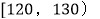 内的概率
内的概率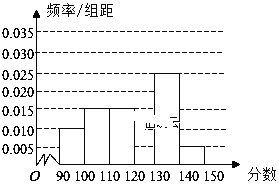
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体
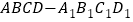 中,
中,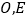 分别为
分别为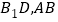 的中点.
的中点.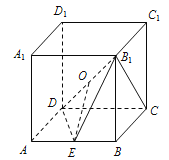
(1)求证:
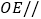 平面
平面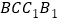 ;
;(2)求证:平面
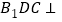 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
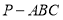 中,平面
中,平面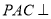 平面
平面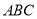 ,
,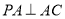 ,
,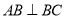 .设
.设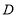 ,
,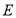 分别为
分别为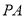 ,
,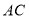 中点.
中点.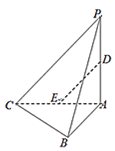
(1)求证:
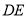
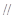 平面
平面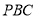 ;
;(2)求证:
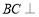 平面
平面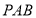 ;
;(3)试问在线段
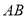 上是否存在点
上是否存在点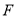 ,使得过三点
,使得过三点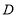 ,
,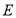 ,
,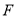 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面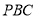 平行?若存在,指出点
平行?若存在,指出点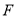 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
相关试题

