【题目】已知过点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
: ![]() 交于M,N两点.
交于M,N两点.
(Ⅰ)设线段MN的中点为P,求点P的轨迹方程;
(Ⅱ)若![]() ,求直线
,求直线![]() 的方程.
的方程.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)设点P的坐标为![]() ,由
,由![]() ,利用坐标运算即可得轨迹方程;
,利用坐标运算即可得轨迹方程;
(Ⅱ)设![]() ,讨论直线
,讨论直线![]() 与
与![]() 轴垂直和存在斜率时两种情况,将
轴垂直和存在斜率时两种情况,将![]() 利用坐标运算结合韦达定理即可求解.
利用坐标运算结合韦达定理即可求解.
试题解析:
(Ⅰ)将![]() 化为标准方程得:
化为标准方程得: ![]() ,
,
可知圆心C的坐标为![]() ,半径
,半径![]() ,
,
设点P的坐标为![]() ,则
,则![]() ,
,
依题意知![]() ,
,
∴![]()
![]()
整理得: ![]() ,
,
∵点A在圆C内部, ∴直线![]() 始终与圆C相交,
始终与圆C相交,
∴点P的轨迹方程为![]() .
.
(Ⅱ)设![]() ,
,
若直线![]() 与
与![]() 轴垂直,则
轴垂直,则![]() 的方程为
的方程为![]() ,代入
,代入![]()
得![]() ,解得
,解得![]() 或
或![]() ,
,
不妨设![]() ,则
,则![]() ,不符合题设,
,不符合题设,
设直线![]() 的斜率为
的斜率为![]() ,则
,则![]() 的方程为
的方程为![]() ,
,
由![]() 消去
消去![]() 得:
得: ![]() ,
,
![]() ,
,
则![]() ,
,
由![]() 得
得![]() ,
,
∴![]()
![]() ,
,
解得: ![]() ,
,
∴当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】将圆
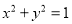 上每一点的纵坐标不变,横坐标变为原来的
上每一点的纵坐标不变,横坐标变为原来的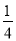 ,得曲线C.
,得曲线C.(Ⅰ)写出C的参数方程;
(Ⅱ)设直线l:
 与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,已知点D在BC边上,满足AD⊥AC,cos ∠BAC=-
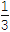 ,AB=3
,AB=3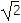 ,BD=
,BD=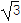 .
.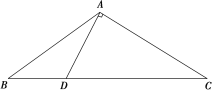
(1)求AD的长;
(2)求△ABC的面积.
-
科目: 来源: 题型:
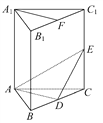
查看答案和解析>>【题目】如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1.
(2)直线A1F∥平面ADE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校艺术节对同一类的
 ,
, ,
,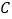 ,
,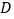 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是
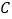 或
或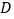 作品获得一等奖”;
作品获得一等奖”;乙说:“
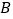 作品获得一等奖”;
作品获得一等奖”;丙说:“
 ,
,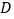 两项作品未获得一等奖”;
两项作品未获得一等奖”;丁说:“是
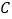 作品获得一等奖”.
作品获得一等奖”.若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2-8y+12=0,直线l经过点D(-2,0),且斜率为k.
(1)求以线段CD为直径的圆E的方程.
(2)若直线l与圆C相离,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2016高考山东理数】已知
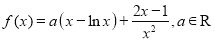 .
.(I)讨论
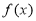 的单调性;
的单调性;(II)当
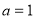 时,证明
时,证明 对于任意的
对于任意的 成立.
成立.
相关试题

