【题目】如图在△ABC中,已知点D在BC边上,满足AD⊥AC,cos ∠BAC=-![]() ,AB=3
,AB=3![]() ,BD=
,BD=![]() .
.
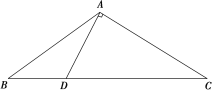
(1)求AD的长;
(2)求△ABC的面积.
参考答案:
【答案】见解析
【解析】(1)因为AD⊥AC,cos ∠BAC=-![]() ,
,
所以sin ∠BAC=![]() .
.
又sin ∠BAC=sin![]() =cos ∠BAD=
=cos ∠BAD=![]() ,
,
在△ABD中,BD2=AB2+AD2-2AB·AD·cos ∠BAD,
即AD2-8AD+15=0,
解得AD=5或AD=3,由于AB>AD,
所以AD=3.
(2)在△ABD中,![]() =
=![]() ,
,
又由cos ∠BAD=![]() 得sin ∠BAD=
得sin ∠BAD=![]() ,所以sin ∠ADB=
,所以sin ∠ADB=![]() ,则sin ∠ADC=sin(π-∠ADB)=sin ∠ADB=
,则sin ∠ADC=sin(π-∠ADB)=sin ∠ADB=![]() .
.
因为∠ADB=∠DAC+∠C=![]() +∠C,所以cos ∠C=
+∠C,所以cos ∠C=![]() .
.
在Rt△ADC中,cos ∠C=![]() ,则tan ∠C=
,则tan ∠C=![]() =
=![]() =
=![]() ,
,
所以AC=3![]() ,
,
则△ABC的面积S=![]() AB·AC·sin ∠BAC=
AB·AC·sin ∠BAC=![]() ×3
×3![]() ×3
×3![]() ×
×![]() =6
=6![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2014全国1理21】设函数
 ,曲线
,曲线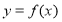 在点
在点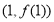 处的切线方程为
处的切线方程为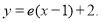
(I)求
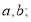
(II)证明:
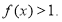
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由9名高二级学生和6名高一级学生组成,现采用分层抽样的方法抽取5人,组成一个体验小组去市场体验“共享单车”的使用.问:
(Ⅰ)应从该兴趣小组中抽取高一级和高二级的学生各多少人;
(Ⅱ)已知该地区有
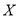 ,
,  两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租
两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租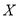 型车,高一级学生都租
型车,高一级学生都租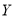 型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租
型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租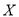 型车的概率.
型车的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】将圆
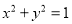 上每一点的纵坐标不变,横坐标变为原来的
上每一点的纵坐标不变,横坐标变为原来的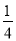 ,得曲线C.
,得曲线C.(Ⅰ)写出C的参数方程;
(Ⅱ)设直线l:
 与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程. -
科目: 来源: 题型:
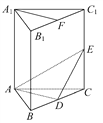
查看答案和解析>>【题目】如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1.
(2)直线A1F∥平面ADE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点
 的动直线
的动直线 与圆
与圆 :
:  交于M,N两点.
交于M,N两点.(Ⅰ)设线段MN的中点为P,求点P的轨迹方程;
(Ⅱ)若
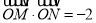 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校艺术节对同一类的
 ,
,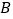 ,
,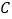 ,
,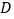 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是
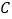 或
或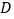 作品获得一等奖”;
作品获得一等奖”;乙说:“
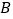 作品获得一等奖”;
作品获得一等奖”;丙说:“
 ,
,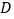 两项作品未获得一等奖”;
两项作品未获得一等奖”;丁说:“是
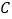 作品获得一等奖”.
作品获得一等奖”.若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
相关试题

