【题目】如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1 , AB⊥AN,CB=BA=AN= ![]() BB1 .
BB1 . 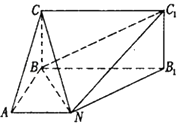
(1)求证:BN⊥平面C1B1N;
(2)求二面角C﹣C1N﹣B的大小.
参考答案:
【答案】
(1)证明:∵四边形BB1C1C是矩形,∴BC⊥BB1,
∵平面BB1C1C⊥底面ABB1N,平面BB1C1C∩底面ABB1N=BB1,BC平面BB1C1C,
∴BC⊥平面ABB1N,
以B为原点,以BA,BB1,BC为坐标轴建立空间直角坐标系B﹣xyz,
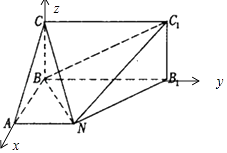
设AB=1,则B(0,0,0),N(1,1,0),B1(0,2,0),C1(0,2,1),C(0,0,1)
∴ ![]() =(1,1,0),
=(1,1,0), ![]() =(﹣1,1,0),
=(﹣1,1,0), ![]() =(0,0,1),
=(0,0,1),
∴ ![]() =﹣1+1=0,
=﹣1+1=0, ![]() =0,
=0,
∴BN⊥NB1,BN⊥B1C1,又NB1∩B1C1=B1,
∴BN⊥平面C1B1N.
(2)解: ![]() =(﹣1,1,1),
=(﹣1,1,1), ![]() =(﹣1,﹣1,1),
=(﹣1,﹣1,1), ![]() =(0,2,0),
=(0,2,0),
设平面BNC1的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 ![]() ,
, ![]() =0,
=0,
∴ ![]() ,令x=1得
,令x=1得 ![]() =(1,﹣1,2),
=(1,﹣1,2),
同理可得平面CNC1的法向量为 ![]() =(1,0,1),
=(1,0,1),
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∴二面角C﹣C1N﹣B的大小为30°.
【解析】(1)证明BC⊥平面ABB1N,建立空间直角坐标系,利用向量证明BN⊥NB1,BN⊥B1C1,从而可证明BN⊥平面C1B1N;(2)分别求出平面BNC1和平面CNC1的法向量,计算法向量的夹角,从而可得二面角C﹣C1N﹣B的大小.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
【答案】(1)
 ;(2)
;(2)
【解析】试题分析:(1)根据中点坐标公式求出
 中点
中点 的坐标,根据斜率公式可求得
的坐标,根据斜率公式可求得 的斜率,利用点斜式可求
的斜率,利用点斜式可求 边上的中线所在直线的方程;(2)先根据斜率公式求出
边上的中线所在直线的方程;(2)先根据斜率公式求出 的斜率,从而求出
的斜率,从而求出 边上的高所在直线的斜率为
边上的高所在直线的斜率为 ,利用点斜式可求
,利用点斜式可求 边上的高所在直线的方程.
边上的高所在直线的方程.试题解析:(1)由B(10,4),C(2,-4),得BC中点D的坐标为(6,0),
所以AD的斜率为k=
 =8,
=8, 所以BC边上的中线AD所在直线的方程为y-0=8(x-6),
即8x-y-48=0.
(2)由B(10,4),C(2,-4),得BC所在直线的斜率为k=
 =1,
=1, 所以BC边上的高所在直线的斜率为-1,
所以BC边上的高所在直线的方程为y-8=-(x-7),即x+y-15=0.
【题型】解答题
【结束】
17【题目】已知直线l:x-2y+2m-2=0.
(1)求过点(2,3)且与直线l垂直的直线的方程;
(2)若直线l与两坐标轴所围成的三角形的面积大于4,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】第35届牡丹花会期间,我班有5名学生参加志愿者服务,服务场所是王城公园和牡丹公园.
(1)若学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有多少种不同的分配方案?
(2)每名学生都被随机分配到其中的一个公园,设X,Y分别表示5名学生分配到王城公园和牡丹公园的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列和数学期望E(ξ) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x﹣2)ex+a(x+2)2(x>0).
(1)若f(x)是(0,+∞)的单调递增函数,求实数a的取值范围;
(2)当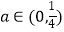 时,求证:函数f(x)有最小值,并求函数f(x)最小值的取值范围.
时,求证:函数f(x)有最小值,并求函数f(x)最小值的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为
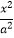 +
+ 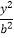 =1(a>b>0),双曲线
=1(a>b>0),双曲线 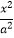 ﹣
﹣ 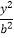 =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 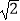 .
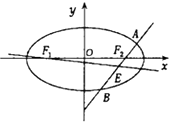
.
(1)求椭圆C的方程;
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=xlnx+ax,a∈R.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若对x>1,f(x)>(b+a﹣1)x﹣b恒成立,求整数b的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差不为0的等差数列{an}的前n项和为Sn,满足S3=a4+4,且a2,a6,a18成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=
 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
相关试题

