【题目】已知函数![]() ,当
,当![]() 时,恒有
时,恒有![]() .当
.当![]() 时,
时, ![]() .
.
(Ⅰ)求证: ![]() 是奇函数;
是奇函数;
(Ⅱ)若![]() ,试求
,试求![]() 在区间
在区间![]() 上的最值;
上的最值;
(Ⅲ)是否存在![]() ,使
,使![]() 对于任意
对于任意![]() 恒成立?若存在,求出实数
恒成立?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
参考答案:
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
. ![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】试题分析:(1)令x=y=0,求出 f(0),令y=-x,可以得出f(-x)与f(x)的关系,从而判断出函数的奇偶性;(2)先判断函数的单调性,取值![]() ,赋值
,赋值![]() ,得出
,得出![]() ,根据
,根据![]() ,利用已知当
,利用已知当![]() 时,
时, ![]() .比较出
.比较出![]() 与
与![]() 的大小,得出函数为增函数,求出函数在区间
的大小,得出函数为增函数,求出函数在区间![]() 上的最值;(3)根据函数为奇函数且为增函数,转化不等式,利用换元法简化不等式,利用极值原理求出m 的范围.
上的最值;(3)根据函数为奇函数且为增函数,转化不等式,利用换元法简化不等式,利用极值原理求出m 的范围.
试题解析:
(Ⅰ)令![]() ,则
,则![]() ,
,
∴![]() .令
.令![]() ,则
,则![]() ,
,
∴![]() ,即
,即![]() 为奇函数;
为奇函数;
(Ⅱ)任取![]() ,且
,且![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵当![]() 时,
时, ![]() ,且
,且![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() 为增函数,
为增函数,
∴当![]() 时,函数有最小值,
时,函数有最小值, ![]() .
.
当![]() 时,函数有最大值,
时,函数有最大值, ![]() ;
;
(Ⅲ)∵函数![]() 为奇函数,
为奇函数,
∴不等式![]()
可化为![]() ,
,
又∵![]() 为增函数,∴
为增函数,∴![]() ,
,
令![]() ,则
,则![]() ,
,
问题转化为![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,只需
,只需![]() ,
,
而![]() ,
,
∴当![]() 时,
时, ![]() ,则
,则![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
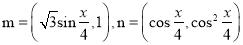 ,记
,记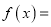
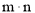 .
.(Ⅰ)求
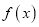 的单调递减区间;
的单调递减区间;(Ⅱ)若
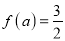 ,求
,求 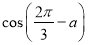 的值;
的值;(Ⅲ)将函数
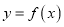 的图象向右平移
的图象向右平移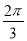 个单位得到
个单位得到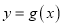 的图象,若函数
的图象,若函数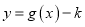 在
在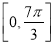 上有零点,求实数
上有零点,求实数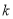 的取值范围.
的取值范围. -
科目: 来源: 题型:
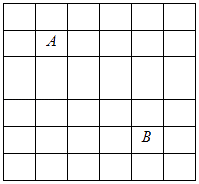
查看答案和解析>>【题目】如图所示在6×6的方格中,有A,B两个格子,则从该方格表中随机抽取一个矩形,该矩形包含格子A但不包含格子B的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】电商中“猫狗大战”在节日期间的竞争异常激烈,在刚过去的618全民年中购物节中,某东当日交易额达1195亿元,现从该电商“剁手党”中随机抽取100名顾客进行回访,按顾客的年龄分成了6组,得到如下所示的频率直方图.
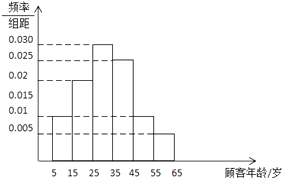
(1)求顾客年龄的众数,中位数,平均数(每一组数据用中点做代表);
(2)用样本数据的频率估计总体分布中的概率,则从全部顾客中任取3人,记随机变量X为顾客中年龄小于25岁的人数,求随机变量X的分布列以及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C极坐标方程:
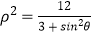 ,点P极坐标为
,点P极坐标为 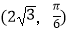 ,直线l过点P,且倾斜角为
,直线l过点P,且倾斜角为  .
.
(1)求曲线C的直角坐标方程及直线l参数方程;
(2)若直线l与曲线C交于A,B两点,求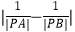 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某游乐园的摩天轮最高点距离地面108米,直径长是98米,均速旋转一圈需要18分钟.如果某人从摩天轮的最低点
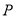 处登上摩天轮并开始计时,那么:
处登上摩天轮并开始计时,那么: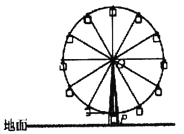
(1)当此人第四次距离地面
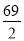 米时用了多少分钟?
米时用了多少分钟?(2)当此人距离地面不低于
 米时可以看到游乐园的全貌,求摩天轮旋转一圈中有多少分钟可以看到游乐园的全貌?
米时可以看到游乐园的全貌,求摩天轮旋转一圈中有多少分钟可以看到游乐园的全貌? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)若
 ,判断函数
,判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;(2)若函数
 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;(3)若存在实数
 使得关于
使得关于 的方程
的方程 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数 的取值范围.
的取值范围.
相关试题

