【题目】随机抽取了40辆汽车在经过路段上某点时的车速(km/h),现将其分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图所示的频率分布直方图.
,后得到如图所示的频率分布直方图.
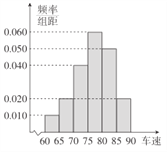
(Ⅰ)现有某汽车途经该点,则其速度低于80km/h的概率约是多少?
(Ⅱ)根据直方图可知,抽取的40辆汽车经过该点的平均速度约是多少?
(Ⅲ)在抽取的40辆且速度在![]() (km/h)内的汽车中任取2辆,求这2辆车车速都在
(km/h)内的汽车中任取2辆,求这2辆车车速都在![]() (km/h)内的概率.
(km/h)内的概率.
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() (km/h);(III)
(km/h);(III)![]() .
.
【解析】试题分析:(Ⅰ) ![]() 表示80
表示80 ![]() 左边小矩形的和;(Ⅱ)根据频率分布直方图计算平均车速就是每个小矩形的中点值乘以本组的频率(本组小矩形的面积)和;(Ⅲ)分别计算车速在
左边小矩形的和;(Ⅱ)根据频率分布直方图计算平均车速就是每个小矩形的中点值乘以本组的频率(本组小矩形的面积)和;(Ⅲ)分别计算车速在![]() 和
和![]() 的车辆,然后再分别编号,列举所有抽取2辆车的基本事件,再计算两辆车都落在区间
的车辆,然后再分别编号,列举所有抽取2辆车的基本事件,再计算两辆车都落在区间![]() 的基本事件的个数,相除就是概率.
的基本事件的个数,相除就是概率.
试题解析:(Ⅰ)速度低于80km/h的概率约为: ![]() .
.
(Ⅱ)这40辆小型车辆的平均车速为:
![]() (km/h),
(km/h),
(Ⅲ)车速在![]() 内的有2辆,记为
内的有2辆,记为![]() 车速在
车速在![]() 内的有4辆,记为
内的有4辆,记为![]() ,从中抽2辆,抽法为
,从中抽2辆,抽法为![]() 共15种,
共15种,
其中车速都在![]() 内的有6种,故所求概率
内的有6种,故所求概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.
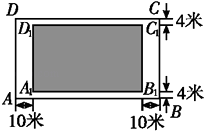
(1)若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
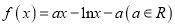 .
.(Ⅰ)讨论函数
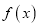 的单调性;
的单调性;(Ⅱ)或
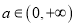 ,
,  时,证明:
时,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 过点
过点 ,顺次连接椭圆的四个顶点得到的四边形的面积为
,顺次连接椭圆的四个顶点得到的四边形的面积为 ,点
,点 .
.(Ⅰ)求椭圆
 的方程.
的方程.(Ⅱ)已知点
 ,是椭圆
,是椭圆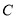 上的两点.
上的两点.(ⅰ)若
 ,且
,且 为等边三角形,求
为等边三角形,求 的面积;
的面积;(ⅱ)若
 ,证明:
,证明:  不可能为等边三角形.
不可能为等边三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的通项为an , 前n项和为sn , 且an是sn与2的等差中项,数列{bn}中,b1=1,点P(bn , bn+1)在直线x﹣y+2=0上. (Ⅰ)求数列{an}、{bn}的通项公式an , bn
(Ⅱ)设{bn}的前n项和为Bn , 试比较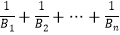 与2的大小.
与2的大小.
(Ⅲ)设Tn=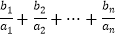 ,若对一切正整数n,Tn<c(c∈Z)恒成立,求c的最小值.
,若对一切正整数n,Tn<c(c∈Z)恒成立,求c的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
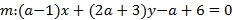 ,
, 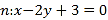 .
.(1)当
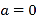 时,直线
时,直线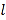 过
过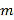 与
与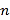 的交点,且它在两坐标轴上的截距相反,求直线
的交点,且它在两坐标轴上的截距相反,求直线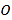 的方程;
的方程;(2)若坐标原点
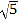 到直线
到直线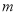 的距离为
的距离为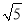 ,判断
,判断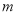 与
与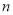 的位置关系.
的位置关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
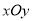 中,以
中,以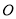 为极点,
为极点, 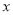 轴的正半轴为极轴建立极坐标系.若直线
轴的正半轴为极轴建立极坐标系.若直线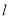 的极坐标方程为
的极坐标方程为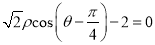 ,曲线
,曲线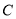 的极坐标方程为
的极坐标方程为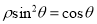 ,将曲线
,将曲线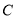 上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线
上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线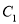 .
.(Ⅰ)求曲线
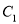 的直角坐标方程;
的直角坐标方程;(Ⅱ)已知直线
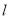 与曲线
与曲线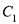 交于
交于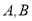 两点,点
两点,点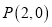 ,求
,求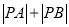 的值.
的值.
相关试题

