(本小题满分12分)已知函数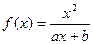 (a,b为常数)且方程f(x)-x+12=0
(a,b为常数)且方程f(x)-x+12=0
有两个实根为x1="3," x2=4.(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;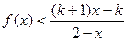 .
.
参考答案:
解:(1)将 得
得
(2)不等式即为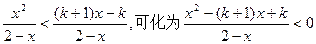
即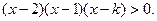
①当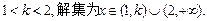
②当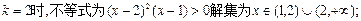
③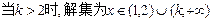 .
.
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)函数
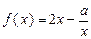 的定义域为
的定义域为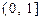 (
(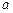 为实数).
为实数).
(1)当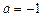 时,求函数
时,求函数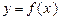 的值域;
的值域;
(2)若函数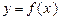 在定义域上是减函数,求
在定义域上是减函数,求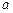 的取值范围;
的取值范围;
(3)函数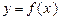 在
在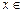
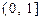 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时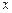 的值.
的值. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分14分)设二次函数
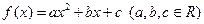 满足下列条件:
满足下列条件:
①当 ∈R时,
∈R时, 的最小值为0,且f (
的最小值为0,且f ( -1)=f(-
-1)=f(- -1)成立;
-1)成立;
②当 ∈(0,5)时,
∈(0,5)时, ≤
≤ ≤2
≤2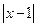 +1恒成立。
+1恒成立。
(1)求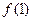 的值;
的值;
(2)求 的解析式;
的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当 ∈
∈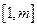 时,就有
时,就有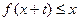 成立。
成立。 -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)二次函数f(x)满足
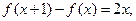 且f(0)=1.
且f(0)=1.
(1)求f(x)的解析式;
(2)在区间 上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知某商品的价格上涨x%,销售的数量就减少mx%,其中m为正的常数。
(1)当m=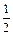 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?
(2)如果适当地涨价,能使销售总金额增加,求m的取值范围 -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分14分)已知函数
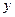 =
=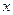 +
+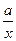 有如下性质:如果常数
有如下性质:如果常数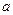 >0,那么该
>0,那么该
函数在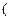 0,
0,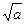
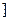 上是减函数,在
上是减函数,在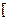
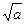 ,+∞
,+∞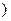 上是增函数.
上是增函数.
(1)如果函数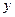 =
=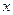 +
+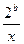 (
(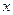 >0)的值域为
>0)的值域为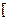 6,+∞
6,+∞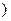 ,求
,求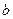 的值;
的值;
(2)研究函数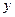 =
=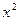 +
+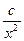 (常数
(常数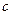 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(3)对函数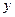 =
=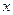 +
+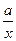 和
和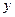 =
=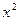 +
+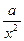 (常数
(常数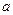 >0)作出推广,使它们都是你所推广的
>0)作出推广,使它们都是你所推广的
函数的特例.
(4)(理科生做)研究推广后的函数的单调性(只须写出结论,不必证明),并求函数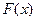 =
=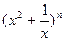 +
+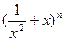 (
(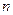 是正整数)在区间[
是正整数)在区间[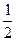 ,2]上的最大值和最小值(可利用你
,2]上的最大值和最小值(可利用你
的研究结论). -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知
 的反函数为
的反函数为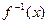 ,
, .
.
(1)若 ,求
,求 的取值范围D;
的取值范围D;
(2)设函数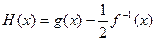 ,当
,当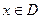 时,求函数
时,求函数 的值域.
的值域.
相关试题

