(本小题满分14分)设二次函数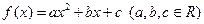 满足下列条件:
满足下列条件:
①当 ∈R时,
∈R时, 的最小值为0,且f (
的最小值为0,且f ( -1)=f(-
-1)=f(- -1)成立;
-1)成立;
②当 ∈(0,5)时,
∈(0,5)时, ≤
≤ ≤2
≤2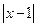 +1恒成立。
+1恒成立。
(1)求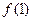 的值;
的值;
(2)求 的解析式;
的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当 ∈
∈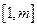 时,就有
时,就有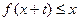 成立。
成立。
参考答案:
解: (1)在②中令x=1,有1≤f(1)≤1,故f(1)=1…………………………3分
(2)由①知二次函数的关于直线x=-1对称,且开口向上
故设此二次函数为f(x)=a(x+1)2,(a>0),∵f(1)=1,∴a=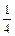
∴f(x)= 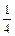 (x+1)2 …………………………7分
(x+1)2 …………………………7分
(3)假设存在t∈R,只需x∈[1,m],就有f(x+t)≤x.
f(x+t)≤x
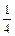 (x+t+1)2≤x
(x+t+1)2≤x x2+(2t-2)x+t2+2t+1≤0.
x2+(2t-2)x+t2+2t+1≤0.
令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,m].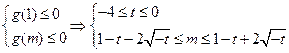
∴m≤1-t+2 ≤1-(-4)+2
≤1-(-4)+2 =9
=9
t=-4时,对任意的x∈[1,9]
恒有g(x)≤0, ∴m的最大值为9. ………………………… 14分
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>(Ⅰ)计算:
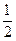 lg2+
lg2+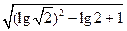 -
-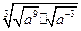 ÷
÷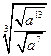 ;
;
(Ⅱ)已知lga+lgb=21g(a-2b),求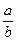 的值.
的值. -
科目: 来源: 题型:解答题
查看答案和解析>>(本题满分14分)若定义在
 上的函数
上的函数 同时满足下列三个条件:
同时满足下列三个条件:
①对任意实数 均有
均有 成立;
成立;
②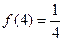 ;
;
③当 时,都有
时,都有 成立。
成立。
(1)求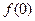 ,
, 的值;
的值;
(2)求证: 为
为 上的增函数
上的增函数
(3)求解关于 的不等式
的不等式 .
. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)函数
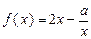 的定义域为
的定义域为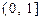 (
(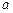 为实数).
为实数).
(1)当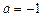 时,求函数
时,求函数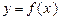 的值域;
的值域;
(2)若函数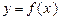 在定义域上是减函数,求
在定义域上是减函数,求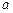 的取值范围;
的取值范围;
(3)函数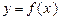 在
在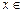
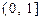 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时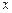 的值.
的值. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)二次函数f(x)满足
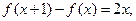 且f(0)=1.
且f(0)=1.
(1)求f(x)的解析式;
(2)在区间 上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知函数
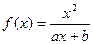 (a,b为常数)且方程f(x)-x+12=0
(a,b为常数)且方程f(x)-x+12=0
有两个实根为x1="3," x2=4.(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;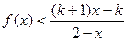 .
. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知某商品的价格上涨x%,销售的数量就减少mx%,其中m为正的常数。
(1)当m=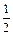 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?
(2)如果适当地涨价,能使销售总金额增加,求m的取值范围
相关试题

