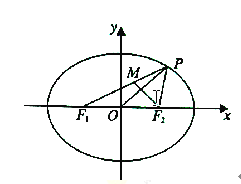
【题目】如图所示,已知椭圆![]() :
:![]() ,其中
,其中![]() ,
,![]() ,
,![]() 分别为其左,右焦点,点
分别为其左,右焦点,点![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() ,且
,且![]() .
.
(1)当![]() ,
,![]() ,且
,且![]() 时,求
时,求![]() 的值;
的值;
(2)若![]() ,试求椭圆
,试求椭圆![]() 离心率
离心率![]() 的范围.
的范围.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析: (1)先根据![]() 确定点
确定点![]() 坐标,由
坐标,由![]() 可得点
可得点![]() 坐标(用
坐标(用![]() 表示),最后根据
表示),最后根据![]() ,利用斜率乘积为
,利用斜率乘积为![]() ,列方程求
,列方程求![]() 的值;(2)设
的值;(2)设![]() ,由
,由![]() 可得点
可得点![]() 坐标(用
坐标(用![]() 表示),由
表示),由![]() ,得
,得![]() 一组关系,再根据点
一组关系,再根据点![]() 在椭圆
在椭圆![]() 上,可解得
上,可解得![]() (用
(用![]() 表示),最后根据
表示),最后根据![]() 取值范围建立
取值范围建立![]() 之间关系,求得离心率
之间关系,求得离心率![]() 的范围.
的范围.
试题解析:(1)当![]() ,
,![]() 时,椭圆
时,椭圆![]() 为:
为:![]() ,
,![]() ,
,![]() ,
,
∴![]() ,则
,则![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
直线![]() :
:![]() ,①
,①
直线![]() :
:![]() ,②
,②
联立①②解得![]() ,
,
∴![]() .
.
同理可得当![]() 时,
时,![]() ,
,
综上所述,![]() .
.
(2)设![]() ,
,![]() ,
,
由![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
由![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,③
,③
又![]() ,④
,④
联立③④解得![]() (舍)或
(舍)或![]() (∵
(∵![]() ),
),
∴![]() ,即
,即![]() ,
,
∴![]() ,故
,故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知边长为
 米的正方形钢板有一个角被锈蚀,其中
米的正方形钢板有一个角被锈蚀,其中 米,
米,  米.为了合理利用这块钢板,将在五边形
米.为了合理利用这块钢板,将在五边形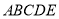 内截取一个矩形块
内截取一个矩形块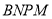 ,使点
,使点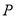 在边
在边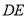 上.
上.
(1)设
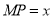 米,
米, 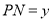 米,将
米,将 表示成
表示成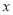 的函数,求该函数的解析式及定义域;
的函数,求该函数的解析式及定义域;(2)求矩形
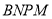 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
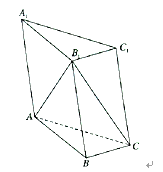
查看答案和解析>>【题目】如图所示,已知三棱柱
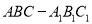 中,
中, 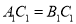 ,
, 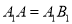 ,
,  .
.
(1)求证:
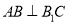 ;
;(2)若
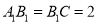 ,
, 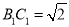 ,求二面角
,求二面角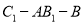 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次国际学术会议上,来自四个国家的五位代表被安排坐在一张圆桌,为了使他们能够自由交谈,事先了解到的情况如下:
甲是中国人,还会说英语.
乙是法国人,还会说日语.
丙是英国人,还会说法语.
丁是日本人,还会说汉语.
戊是法国人,还会说德语.
则这五位代表的座位顺序应为( )
A. 甲丙丁戊乙 B. 甲丁丙乙戊
C. 甲乙丙丁戊 D. 甲丙戊乙丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
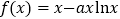 (
(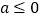 ),
),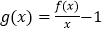 .
.(1)求函数
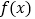 单调区间;
单调区间;(2)当
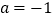 时,
时,①求函数
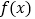 在
在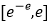 上的值域;
上的值域;②求证:
 ,其中
,其中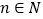 ,
,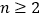 .(参考数据
.(参考数据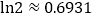 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
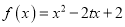 ,
, 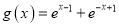 ,且函数
,且函数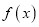 的图象关于直线
的图象关于直线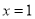 对称。
对称。(1)求函数
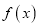 在区间
在区间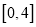 上最大值;
上最大值;(2)设
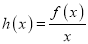 ,不等式
,不等式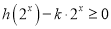 在
在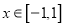 上恒成立,求实数
上恒成立,求实数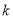 的取值范围;
的取值范围;(3)设
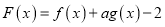 有唯一零点,求实数
有唯一零点,求实数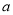 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过
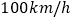 的有20人,不超过
的有20人,不超过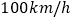 的有10人.在20名女性驾驶员中,平均车速超过
的有10人.在20名女性驾驶员中,平均车速超过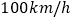 的有5人,不超过
的有5人,不超过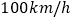 的有15人.
的有15人.(Ⅰ)完成下面的列联表,并判断是否有
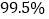 的把握认为平均车速超过
的把握认为平均车速超过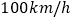 的人与性别有关;
的人与性别有关;平均车数超过
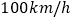 人数
人数平均车速不超过
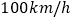 人数
人数合计
男性驾驶员人数
女性驾驶员人数
合计
(Ⅱ)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随即抽取3辆,记这3辆车中驾驶员为女性且车速不超过
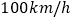 的车辆数为
的车辆数为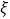 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求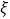 的分布列和数学期望
的分布列和数学期望参考公式:
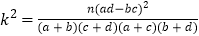 ,其中
,其中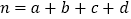 .
.参考数据:
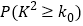
0.150
0.100
0.05
0.025
0.010
0.005
0.001
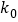
2.072
2.706
3.841
5.024
6.635
7.879
10.828
相关试题

