【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)函数![]() 的图象与
的图象与![]() 的图象无公共点,求实数
的图象无公共点,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,请求出整数
的图象的下方?若存在,请求出整数![]() 的最大值;若不存在,请说理由.
的最大值;若不存在,请说理由.
(参考数据:![]() ,
,![]() ,
,![]() ).
).
参考答案:
【答案】(Ⅰ)![]() ,(Ⅱ)1
,(Ⅱ)1
【解析】
试题分析:(Ⅰ)函数图象无公共点,可以转化为方程![]() 无实根,此方程可用分离参数法化为
无实根,此方程可用分离参数法化为![]() 无实根,从而只要求出函数
无实根,从而只要求出函数![]() 的值域即可,这可导数的知识求得;(Ⅱ)同样问题转化为“不等式
的值域即可,这可导数的知识求得;(Ⅱ)同样问题转化为“不等式![]() 对
对![]() 恒成立”,即
恒成立”,即![]() 对
对![]() 恒成立,因此问题转化为
恒成立,因此问题转化为
求函数![]() 的最小值.
的最小值.
试题解析:(Ⅰ)函数![]() 与
与![]() 无公共点,
无公共点,
等价于方程![]() 在
在![]() 无解
无解
令![]() ,则
,则![]() 令
令![]() 得
得![]()
|
|
|
|
| + | 0 | - |
| 增 | 极大值 | 减 |
因为![]() 是唯一的极大值点,故
是唯一的极大值点,故![]()
故要使方程![]() 在
在![]() 无解,
无解,
当且仅当![]() ,故实数
,故实数![]() 的取值范围为
的取值范围为![]()
(Ⅱ)假设存在实数![]() 满足题意,则不等式
满足题意,则不等式![]() 对
对![]() 恒成立.
恒成立.
即![]() 对
对![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
∵![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,![]() ,
,
且![]() 的图象在
的图象在![]() 上连续,
上连续,
∴存在![]() ,使得
,使得![]() ,即
,即![]() ,则
,则![]() ,
,
∴ 当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增,
单调递增,
则![]() 取到最小值
取到最小值![]()
 ,
,
∴ ![]() ,即
,即![]() 在区间
在区间![]() 内单调递增.
内单调递增.
![]() ,
,
∴存在实数![]() 满足题意,且最大整数
满足题意,且最大整数![]() 的值为
的值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
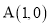 ,点
,点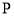 是圆
是圆
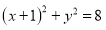 上的任意一点,线段
上的任意一点,线段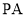 的垂直平分线与直线
的垂直平分线与直线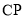 交于点
交于点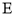 .
.(Ⅰ)求点
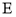 的轨迹方程;
的轨迹方程;(Ⅱ)若直线
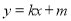 与点
与点 的轨迹有两个不同的交点
的轨迹有两个不同的交点 和
和 ,且原点
,且原点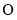 总在以
总在以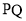 为直径的圆的内部,求实数
为直径的圆的内部,求实数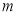 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点
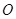 的椭圆
的椭圆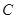 经过点
经过点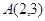 ,且点
,且点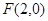 为其右焦点.
为其右焦点.(Ⅰ)求椭圆
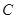 的标准方程;
的标准方程;(Ⅱ)是否存在平行于
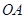 的直线
的直线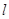 ,使得直线
,使得直线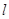 与椭圆
与椭圆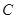 有公共点,且直线
有公共点,且直线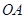 与
与 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某几何体的三视图如图所示,则它的外接球表面积为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆方程
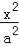 +
+ =1(a>b>0),椭圆上一点到两焦点的距离和为4,过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
=1(a>b>0),椭圆上一点到两焦点的距离和为4,过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.(1)求椭圆方程;
(2)若M,N是椭圆C上的点,且直线OM与ON的斜率之积为﹣
 ,是否存在动点P(x0,y0),若
,是否存在动点P(x0,y0),若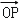 =
=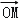 +2
+2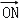 ,有x02+2y02为定值
,有x02+2y02为定值 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知过点
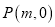 的直线
的直线 的参数方程是
的参数方程是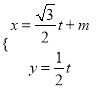 (
(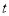 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点,  轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线 的极坐标方程式为
的极坐标方程式为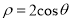 .
.(Ⅰ)求直线
 的普通方程和曲线
的普通方程和曲线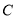 的直角坐标方程;
的直角坐标方程;(Ⅱ)若直线
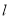 与曲线
与曲线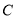 交于两点
交于两点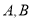 ,且
,且 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取
 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为 ,
, ,
, ,
, ,由此得到样本的重量频率分布直方图(如图).
,由此得到样本的重量频率分布直方图(如图).
(Ⅰ)求
 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;(Ⅱ)从盒子中随机抽取
 个小球,其中重量在
个小球,其中重量在 内的小球个数为
内的小球个数为 ,求
,求 的分布列和数学期望. (以直方图中的频率作为概率).
的分布列和数学期望. (以直方图中的频率作为概率).
相关试题

