【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:
(单位: ![]() )的数据,如下表:
)的数据,如下表:
| 2 | 5 | 8 | 9 | 11 |
| 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地1月份某天的最低气温为6
之间是正相关还是负相关;若该地1月份某天的最低气温为6![]() ,请用所求回归方程预测该店当日的营业额.
,请用所求回归方程预测该店当日的营业额.
附: 回归方程![]() 中,
中,  ,
,![]()
参考答案:
【答案】(1)![]() ;(2)负相关,估值9.56千克.
;(2)负相关,估值9.56千克.
【解析】试题分析:
(1)根据公式求出线性回归直线方程的系数,可得方程;
(2)由回归方程中![]() 的系数的正负确定正相关还是负相关,把
的系数的正负确定正相关还是负相关,把![]() 代入回归直线方程可得估值.
代入回归直线方程可得估值.
试题解析:
(1) ∵令![]() ,则
,则![]() ,
, ![]() ,
, ![]()
∴![]() ∴
∴![]() ,
,
∴![]() ,∴
,∴![]()
∴所求的回归方程是![]()
(2) 由![]() 知
知![]() 与
与![]() 之间是负相关;
之间是负相关;
将![]() 代入回归方程可预测该店当日的销售额
代入回归方程可预测该店当日的销售额![]()
![]() (千克)
(千克)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
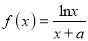 (
(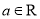 ),曲线
),曲线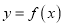 在点
在点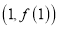 处的切线与直线
处的切线与直线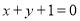 垂直.
垂直.(Ⅰ)试比较
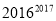 与
与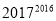 的大小,并说明理由;
的大小,并说明理由;(Ⅱ)若函数
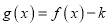 有两个不同的零点
有两个不同的零点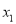 ,
, 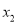 ,证明:
,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
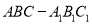 中,
中, 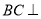 平面
平面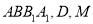 分别为
分别为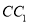 和
和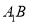 的中点,
的中点, 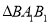 是边长为
是边长为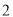 的正三角形,
的正三角形, 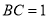 .
.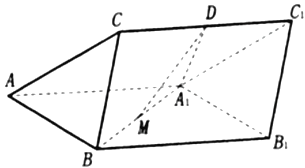
(1)证明:
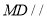 平面
平面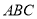 ;
;(2)求二面角
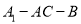 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x2+bx+c,若f(﹣3)=f(1),f(0)=﹣3.
(1)求函数f(x)的解析式;
(2)若函数g(x)=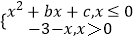 画出函数g(x)图象;
画出函数g(x)图象;
(3)求函数g(x)在[﹣3,1]的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一颗骰子投掷两次分别得到点数a,b,则直线ax-by=0与圆(x-2)2+y2=2相交的概率为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正三棱柱
 中,
中, 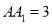 ,
, 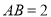 ,
, 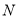 为棱
为棱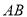 的中点.
的中点.(
 )求证:
)求证: 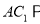 平面
平面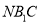 .
.(
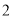 )求证:平面
)求证:平面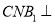 平面
平面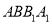 .
.(
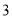 )求四棱锥
)求四棱锥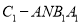 的体积.
的体积.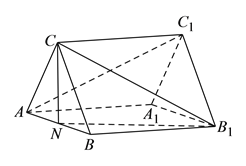
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
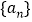 是公差不为零的等差数列,
是公差不为零的等差数列,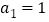 ,且
,且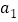 ,
,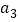 ,
,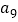 成等比数列.
成等比数列.(1)求数列
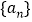 的通项;
的通项;(2)求数列
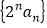 的前
的前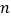 项和
项和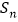 .
.
相关试题

