【题目】已知![]() 是公差不为零的等差数列,
是公差不为零的等差数列,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项;
的通项;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列,建立关于公差
成等比数列,建立关于公差![]() 的方程,解方程可求得
的方程,解方程可求得![]() ,进而求出通项
,进而求出通项![]() ;(2)由(1)可得
;(2)由(1)可得![]() ,根据错位相减法结合等比数列的前
,根据错位相减法结合等比数列的前![]() 项和公式可求数列
项和公式可求数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)由题设知公差![]() .
.
由![]() ,
,![]() ,
,![]() ,
,![]() 成等比数列,得
成等比数列,得![]() ,
,
解得![]() 或
或![]() (舍去),故
(舍去),故![]() 的通项
的通项![]() .
.
(2)![]() ①
①
![]() ,②
,②
①![]() ②得:
②得:![]() ,
,
∴![]() .
.
【易错点晴】本题主要考查等差数列的通项公式、等比数列的求和公式以及“错位相减法”求数列的和,属于难题. “错位相减法”求数列的和是重点也是难点,利用“错位相减法”求数列的和应注意以下几点:①掌握运用“错位相减法”求数列的和的条件(一个等差数列与一个等比数列的积);②相减时注意最后一项的符号;③求和时注意项数别出错;④最后结果一定不能忘记等式两边同时除以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量
 (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温 (单位:
(单位:  )的数据,如下表:
)的数据,如下表:
2
5
8
9
11
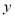
12
10
8
8
7
(1)求出
 与
与 的回归方程
的回归方程 ;
;(2)判断
 与
与 之间是正相关还是负相关;若该地1月份某天的最低气温为6
之间是正相关还是负相关;若该地1月份某天的最低气温为6 ,请用所求回归方程预测该店当日的营业额.
,请用所求回归方程预测该店当日的营业额.附: 回归方程
 中,
中,  ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一颗骰子投掷两次分别得到点数a,b,则直线ax-by=0与圆(x-2)2+y2=2相交的概率为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正三棱柱
 中,
中, 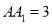 ,
, 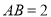 ,
, 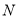 为棱
为棱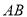 的中点.
的中点.(
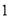 )求证:
)求证: 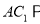 平面
平面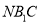 .
.(
 )求证:平面
)求证:平面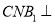 平面
平面 .
.(
 )求四棱锥
)求四棱锥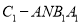 的体积.
的体积.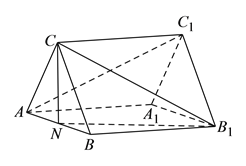
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的偶函数f(x),对任意x1 , x2∈[0,+∞)(x1≠x2),有
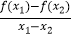 <0,则( )
<0,则( )
A.f(3)<f(﹣2)<f(1)
B.f(1)<f(﹣2)<f(3)
C.f(﹣2)<f(1)<f(3)
D.f(3)<f(1)<f(﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)﹣g(x)=ex , 则有( )
A.f(2)<f(3)<g(0)
B.g(0)<f(3)<f(2)
C.f(2)<g(0)<f(3)
D.g(0)<f(2)<f(3) -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆与双曲线有相同的焦点
 ,
, ,椭圆的一个短轴端点为
,椭圆的一个短轴端点为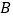 ,直线
,直线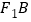 与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为
与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为 ,
, ,则
,则 的最小值为__________.
的最小值为__________.
相关试题

