【题目】已知点F1(﹣1,0),F2(1,0),动点M到点F2的距离是 ![]() ,线段MF1的中垂线交线段MF2于点P. (Ⅰ)当点M变化时,求动点P的轨迹G的方程;
,线段MF1的中垂线交线段MF2于点P. (Ⅰ)当点M变化时,求动点P的轨迹G的方程;
(Ⅱ)过点F2且不与x轴重合的直线L与曲线G相交于A,B两点,过点B作x轴的平行线与直线x=2相交于点C,则直线AC是否恒过定点,若是请求出该定点,若不是请说明理由.
参考答案:
【答案】解:(Ⅰ)∵P在线段MF1的中垂线上,∴PM=PF1 , 又P在线段MF2上,∴PM+PF2=MF2=2 ![]() ,
,
∴PF1+PF2=2 ![]() ,而F1F2=2,
,而F1F2=2,
∴动点P的轨迹G是以F1 , F2为焦点的椭圆,
设椭圆方程为 ![]() ,则2a=2
,则2a=2 ![]() ,c=1,∴a=
,c=1,∴a= ![]() ,b=1,
,b=1,
∴动点P的轨迹方程为 ![]() .
.
(Ⅱ)①当l的斜率不存在时,不妨取 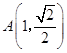 ,
, 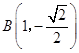 ,
,
∴C(2,﹣ ![]() ),直线AC的方程为
),直线AC的方程为 ![]() x+y﹣
x+y﹣ ![]() =0,
=0,
此时易知AC过点 ![]() .
.
②当l的斜率存在时,设l的方程为:y=k(x﹣1)
联立方程组 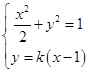 ,消去y得:(1+2k2)x2﹣4k2x+2k2﹣2=0,
,消去y得:(1+2k2)x2﹣4k2x+2k2﹣2=0,
设A(x1 , y1)、B(x2 , y2),则C(2,y2),且x1+x2= ![]() ,
, ![]() ,
,
直线AC方程为 ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= 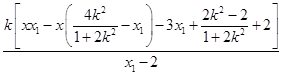 =
= 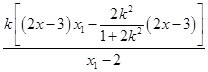 .
.
当 ![]() 时,y=0;
时,y=0;
综上可知,直线AC恒过定点 ![]() .
.
【解析】(I)由中垂线性质可得PM+PF2=MF2=2 ![]() ,故而P点轨迹为F1 , F2为焦点的椭圆,利用定义求出a,b即可得出方程;(II)讨论直线l的斜率,联立方程组,利用根与系数的关系求出直线AC的方程,根据方程判断即可.
,故而P点轨迹为F1 , F2为焦点的椭圆,利用定义求出a,b即可得出方程;(II)讨论直线l的斜率,联立方程组,利用根与系数的关系求出直线AC的方程,根据方程判断即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
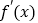 是定义域为
是定义域为 的函数
的函数 的导函数,
的导函数, ,
, ,则
,则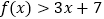 的解集为( )
的解集为( )A.
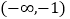 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解人们对城市治安状况的满意度,某部门对城市部分居民的“安全感”进行调查,在调查过程中让每个居民客观地对自己目前生活城市的安全感进行评分,并把所得分作为“安全感指数”,即用区间[0,100]内的一个数来表示,该数越接近100表示安全感越高.现随机对该地区的男、女居民各500人进行了调查,调查数据如表所示:
安全感指数
[0,20)
[20,40)
[40,60)
[60,80)
[80,100]
男居民人数
8
16
226
131
119
女居民人数
12
14
174
122
178
根据表格,解答下面的问题:
(Ⅰ)估算该地区居民安全感指数的平均值;
(Ⅱ)如果居民安全感指数不小于60,则认为其安全感好.为了进一步了解居民的安全感,调查组又在该地区随机抽取3对夫妻进行调查,用X表示他们之中安全感好的夫妻(夫妻二人都感到安全)的对数,求X的分布列及期望(以样本的频率作为总体的概率). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,∠ADC=120°,AB=2CD=2,平面D1DCC1垂直平面ABCD,D1C⊥AB,M是线段AB的中点.
(Ⅰ)求证:D1M∥面B1BCC1;
(Ⅱ)若DD1=2,求平面C1D1M和平面ABCD所成的锐角的余弦值.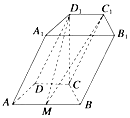
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数

(1)若函数
 是偶函数,求实数
是偶函数,求实数 的取值范围;
的取值范围;(2)若函数
 且任意
且任意 都有
都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
 ,求
,求 在
在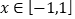 上的最小值
上的最小值 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣
 ,g(x)=
,g(x)=  ﹣1. (Ⅰ)若a>0,试判断f(x)在定义域内的单调性;
﹣1. (Ⅰ)若a>0,试判断f(x)在定义域内的单调性;
(Ⅱ)若f(x)在[1,e]上的最小值为 ,求a的值;
,求a的值;
(Ⅲ)当a=0时,若x≥1时,恒有xf(x)≤λ[g(x)+x]成立,求λ的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)若函数
 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;(2)当
 时,函数
时,函数 图象上的点都在
图象上的点都在 所表示的平面区域内,求实数
所表示的平面区域内,求实数 的取值范围。
的取值范围。
相关试题

