【题目】已知a,b,c分别为△ABC三内角A,B,C的对边,且满足b+ccosA=c+acosC.
(Ⅰ)求角A的大小;
(Ⅱ)若△ABC的面积为 ![]() ,求△ABC的周长的最小值.
,求△ABC的周长的最小值.
参考答案:
【答案】解:(Ⅰ)由正弦定理得:sinB+sinCcosA=sinC+sinAcosC,…(2分)
又sinB=sin(A+C)=sinCcosA+sinAcosC,…(3分)
∴2cosA=1,A为△ABC内角,
∴ ![]() .
.
(Ⅱ)在△ABC中 ![]() ,
,
∴bc=4,
由余弦定理:a2=b2+c2﹣2bccosA=b2+c2﹣bc,
周长 ![]() ,
,
当且仅当b=c=2时等号成立,
故△ABC的周长的最小值为6.
【解析】(Ⅰ)由正弦定理,三角形内角和定理,两角和的正弦函数公式化简已知可得2cosA=1,结合A为△ABC内角,即可得解A的值.(Ⅱ)由已知利用三角形面积公式可求bc=4,由余弦定理,基本不等式即可求得△ABC的周长的最小值.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
 的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a∈R,若x>0时均有[(a﹣1)x﹣1](x2﹣ax﹣1)≥0,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角△ABC中,a,b,c分别是三个内角A,B,C的对边,若2asinB=
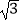 b. (Ⅰ)求A;
b. (Ⅰ)求A;
(Ⅱ)若a=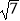 ,△ABC的面积为
,△ABC的面积为 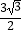 ,求△ABC的周长.
,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产某种产品的年固定成本为250万元,每生产
 千件,需另投入成本为
千件,需另投入成本为 万元,当年产量不足80千件时,
万元,当年产量不足80千件时,  (万元);当年产量不少于80千件时,
(万元);当年产量不少于80千件时,  (万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知p:x∈R,cos2x﹣sinx+2≤m;q:函数
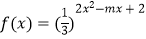 在[1,+∞)上单调递减.
在[1,+∞)上单调递减.
(I)若p∧q为真命题,求m的取值范围;
(II)若p∨q为真命题,p∧q为假命题,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,角A、B、C所对应的边为a,b,c. (I)若sin(A+
 )=
)= 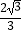 cosA,求A的值;
cosA,求A的值;
(Ⅱ)若cosA= ,b=3c,求sinC的值.
,b=3c,求sinC的值.
相关试题

