【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查了50人,并将调查情况进行整理后制成下表:

(1)规定:年龄在![]() 内的为青年人,年龄在
内的为青年人,年龄在![]() 内的为中年人,根据以上统计数据填写下面
内的为中年人,根据以上统计数据填写下面![]() 列联表:
列联表:

(2)能否在犯错误的概率不超过0.025的前提下,认为赞成“车辆限行”与年龄有关?
参考公式和数据:  ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考答案:
【答案】(1)答案见解析;(2)答案见解析
【解析】试题分析:
(1)由题意统计各个年龄段的人对“车辆限行”的态度填写列联表即可;
(2)结合列联表计算可得: ![]() ,因此,在犯错误的概率不超过0.025的前提下,认为赞成“车辆限行”与年龄有关.
,因此,在犯错误的概率不超过0.025的前提下,认为赞成“车辆限行”与年龄有关.
试题解析:
(1)根据题目中的数据,填写列联表如下:

(2)由(1)表中数据计算得
![]() ,对照临界值得,
,对照临界值得, ![]() ,
,
因此,在犯错误的概率不超过0.025的前提下,认为赞成“车辆限行”与年龄有关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25
 (分贝),并规定测试值在区间
(分贝),并规定测试值在区间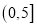 为非常优秀,测试值在区间
为非常优秀,测试值在区间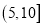 为优秀.某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
为优秀.某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
(Ⅰ)现从听力等级为
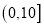 的同学中任意抽取出4人,记听力非常优秀的同学人数为
的同学中任意抽取出4人,记听力非常优秀的同学人数为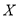 ,求
,求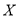 的分布列与数学期望;
的分布列与数学期望;(Ⅱ)在(Ⅰ)中抽出的4人中任选一人参加一个更高级别的听力测试,测试规则如下:四个音叉的发生情况不同,由强到弱的次序分别为1,2,3,4.测试前将音叉随机排列,被测试的同学依次听完后给四个音叉按发音的强弱标出一组序号
 ,
,  ,
, 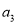 ,
, 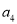 (其中
(其中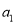 ,
, 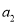 ,
, 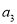 ,
, 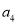 为1,2,3,4的一个排列).若
为1,2,3,4的一个排列).若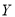 为两次排序偏离程度的一种描述,
为两次排序偏离程度的一种描述, 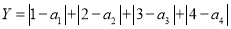 ,求
,求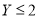 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
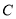 :
: 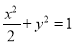 的左顶点为
的左顶点为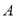 ,右焦点为
,右焦点为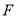 ,
, 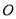 为原点,
为原点, 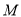 ,
, 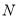 是
是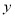 轴上的两个动点,且
轴上的两个动点,且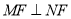 ,直线
,直线 和
和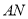 分别与椭圆
分别与椭圆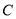 交于
交于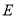 ,
, 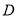 两点.
两点.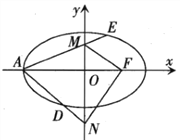
(Ⅰ)求
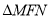 的面积的最小值;
的面积的最小值;(Ⅱ)证明:
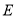 ,
, 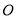 ,
, 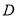 三点共线.
三点共线. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列几种说法: ①若logablog3a=1,则b=3;
②若a+a﹣1=3,则a﹣a﹣1=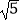 ;
;
③f(x)=log(x+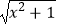 为奇函数;
为奇函数;
④f(x)=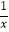 为定义域内的减函数;
为定义域内的减函数;
⑤若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)=log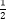 x,其中说法正确的序号为 .
x,其中说法正确的序号为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列命题:
①若
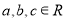 ,则“
,则“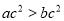 ”是“
”是“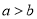 ”成立的充分不必要条件;
”成立的充分不必要条件;②若椭圆
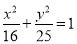 的两个焦点为
的两个焦点为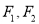 ,且弦
,且弦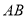 过点
过点 ,则
,则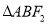 的周长为16;
的周长为16;③若命题“
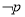 ”与命题“
”与命题“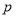 或
或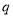 ”都是真命题,则命题
”都是真命题,则命题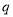 一定是真命题;
一定是真命题;④若命题
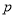 :
: 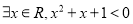 ,则
,则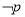 :
: 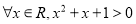
其中为真命题的是__________(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U=R,集合A={x|2x+a>0},B={x|x2﹣2x﹣3>0}. (Ⅰ)当a=2时,求集合A∩B;
(Ⅱ)若A∩(UB)=,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】第十二届全国人名代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为
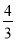 ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.(1)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
(2)根据题意建立
 列联表,并判断是否有99%的把握认为男生与女生对两会的关注有差异?
列联表,并判断是否有99%的把握认为男生与女生对两会的关注有差异?附:
 ,其中
,其中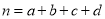 .
.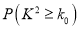
0.100
0.050
0.010
0.001
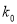
2.706
3.841
6.635
10.828
相关试题

