【题目】(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
参考答案:
【答案】
(1)![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
(2)当![]() 为
为![]() 瓶时,
瓶时,![]() 的数学期望达到最大值。
的数学期望达到最大值。
【解析】
(1)由题意知,![]() 所有的可能取值为200,300,500,由表格数据知
所有的可能取值为200,300,500,由表格数据知
![]()
![]()
![]() .
.
因此![]() 的分布列为
的分布列为
|
|
|
|
| 0.2 | 0.4 | 0.4 |
⑵由题意知,这种酸奶一天的需求量至多为500,至少为200,因此只需考虑![]()
当![]() 时,
时,
若最高气温不低于25,则Y=6n-4n=2n
若最高气温位于区间![]() ,则Y=6×300+2(n-300)-4n=1200-2n;
,则Y=6×300+2(n-300)-4n=1200-2n;
若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n;
因此EY=2n×0.4+(1200-2n)×0.4+(800-2n) ×0.2=640-0.4n
当![]() 时,
时,
若最高气温不低于20,则Y=6n-4n=2n;
若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n;
因此EY=2n×(0.4+0.4)+(800-2n)×0.2=160+1.2n
所以n=300时,Y的数学期望达到最大值,最大值为520元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A、B、C所对的边分别是a、b、c,且a+b+c=8. (Ⅰ)若a=2,b=
 ,求cosC的值;
,求cosC的值;
(Ⅱ)若sinAcos2 +sinBcos2
+sinBcos2  =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S=  sinC,求a和b的值.
sinC,求a和b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}是等差数列,若
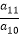 <﹣1,且它的前n项和Sn有最大值,那么当Sn取的最小正值时,n=( )
<﹣1,且它的前n项和Sn有最大值,那么当Sn取的最小正值时,n=( )
A.11
B.17
C.19
D.21 -
科目: 来源: 题型:
查看答案和解析>>【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所称角的最小值为45°;
④直线AB与a所称角的最小值为60°;
其中正确的是________。(填写所有正确结论的编号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x2﹣1|﹣2a+3,下列五个结论:
①当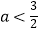 时,函数f(x)没有零点;
时,函数f(x)没有零点;
②当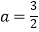 时,函数f(x)有两个零点;
时,函数f(x)有两个零点;
③当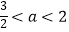 时,函数f(x)有四个零点;
时,函数f(x)有四个零点;
④当a=2时,函数f(x)有三个零点;
⑤当a>2时,函数f(x)有两个零点.
其中正确的结论的序号是 . (填上所有正确结论的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】用an表示自然数n的所有因数中最大的那个奇数,例如:9的因数有1,3,9,则a9=9;10的因数有1,2,5,10,则a10=5,记数列{an}的前n项和为Sn , 则S
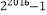 = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:
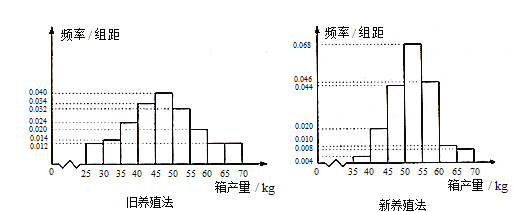
(1) 记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2) 填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg
箱产量≥50kg
旧养殖法
新养殖法
(3) 根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较。
附:
P(
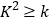 )
)0.050
0.010
0.001
k
3.841
6.635
10.828
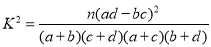

相关试题

