【题目】是否存在实数a,使得函数y=cos2x+asinx+ ![]() ﹣
﹣ ![]() 在闭区间[0,π]的最大值是0?若存在,求出对应的a的值;若不存在,试说明理由.
在闭区间[0,π]的最大值是0?若存在,求出对应的a的值;若不存在,试说明理由.
参考答案:
【答案】解:∵y=cos2x+asinx+ ![]() ﹣
﹣ ![]() =﹣sin2x+asinx+
=﹣sin2x+asinx+ ![]() ﹣
﹣ ![]() , 令sinx=t,t∈[0,1],
, 令sinx=t,t∈[0,1],
∴f(t)=﹣t2+at+ ![]() ﹣
﹣ ![]() ,对称轴为t=
,对称轴为t= ![]() a,
a,
①当a≤0时,函数f(t)在[0,1]上是减函数,
∴f(t)的最大值是g(a)=f(0)= ![]() ﹣
﹣ ![]() =0,解得a=
=0,解得a= ![]() ,不符合题意,
,不符合题意,
②当a≥2时,函数f(t)在[0,1]上是增函数,
∴f(x)的最大值是g(a)=f(1)= ![]() ﹣
﹣ ![]() =0,解得a=
=0,解得a= ![]() ,不符合题意,
,不符合题意,
③当0<a<2时,f(x)在x∈[0,1]的最大值是g( ![]() a)=f(
a)=f( ![]() a)=
a)= ![]() +
+ ![]() ﹣
﹣ ![]() =0,
=0,
解得a=﹣4(舍去),或a= ![]() .·
.·
综上,存在a= ![]() 时,函数在闭区间[0,π]上的最大值是0
时,函数在闭区间[0,π]上的最大值是0
【解析】化简函数f(x),令sinx=t,t∈[0,1],求出f(t)在t∈[0,1]的最大值函数g(a),再令g(a)=0,求对应a的值是否存在即可.
【考点精析】解答此题的关键在于理解三角函数的最值的相关知识,掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
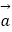 =(m,cos2x),
=(m,cos2x), 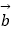 =(sin2x,n),设函数f(x)=
=(sin2x,n),设函数f(x)= 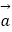
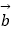 ,且y=f(x)的图象过点(
,且y=f(x)的图象过点( 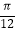 ,
, 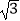 )和点(
)和点( 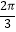 ,﹣2). (Ⅰ)求m,n的值;
,﹣2). (Ⅰ)求m,n的值;
(Ⅱ)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象.若y=g(x)的图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
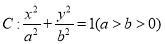 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为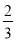 ,短轴长为
,短轴长为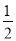 ,直线
,直线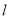 与椭圆
与椭圆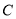 交于
交于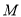 、
、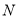 两点.
两点.(1)求椭圆
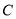 的方程;
的方程; (2)若直线
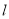 与圆
与圆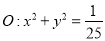 相切,探究
相切,探究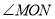 是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,多面体
 中,四边形
中,四边形 是菱形,
是菱形,  ,
,  相交于
相交于 ,
,  ,点
,点 在平面
在平面 上的射影恰好是线段
上的射影恰好是线段 的中点.
的中点.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)若直线
 与平面
与平面 所成的角为
所成的角为 ,求平面
,求平面 与平面
与平面 所成角(锐角)的余弦值.
所成角(锐角)的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )

A.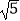
B.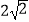
C.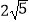
D.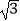
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足log3an+1=log3an+1(n∈N*),且a2+a4+a6=9,则log
 (a5+a7+a9)的值是( )
(a5+a7+a9)的值是( )
A.﹣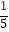
B.﹣5
C.5
D.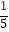
-
科目: 来源: 题型:
查看答案和解析>>【题目】《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即S=
 .现有周长为2
.现有周长为2  +
+  的△ABC满足sinA:sinB:sinC=(
的△ABC满足sinA:sinB:sinC=(  ﹣1):
﹣1):  :(
:(  +1),试用以上给出的公式求得△ABC的面积为( )
+1),试用以上给出的公式求得△ABC的面积为( )
A.
B.
C.
D.
相关试题

