【题目】已知椭圆![]() 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为![]() ,短轴长为
,短轴长为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相切,探究
相切,探究![]() 是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由已知得![]() 由此能求出椭圆
由此能求出椭圆![]() 的方程.
的方程.
(2)当直线![]() 轴时,
轴时, ![]() .当直线
.当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 直线
直线![]() 与与圆
与与圆![]() 的交点M(x1,y1),N(x2,y2),由直线
的交点M(x1,y1),N(x2,y2),由直线![]() 与圆
与圆![]() 相切,得
相切,得![]() ,联立
,联立![]() ,得(
,得(![]() ,由此能证明
,由此能证明![]() 为定值.
为定值.
试题解析:
1)由题意得 ![]()
![]()
(2)当直线![]() 轴时,因为直线与圆相切,所以直线
轴时,因为直线与圆相切,所以直线![]() 方程为
方程为![]()
当![]() 时,得M、N两点坐标分别为
时,得M、N两点坐标分别为![]() ,
,
![]()
当![]() 时,同理
时,同理![]() ;
;
当![]() 与
与![]() 轴不垂直时,
轴不垂直时,
设![]() ,由
,由![]() ,
,
![]() ,
,
联立![]() 得
得![]()
![]() ,
, ![]() ,
, ![]() =
=![]()
![]()
综上, ![]() (定值)
(定值)
-
科目: 来源: 题型:
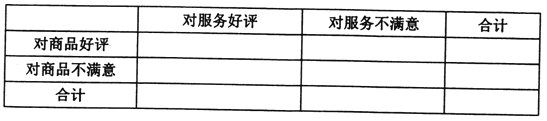
查看答案和解析>>【题目】现如今,“网购”一词不再新鲜,越来越多的人已经接受并喜欢了这种购物方式,但随之也出现了商品质量不能保证与信誉不好等问题,因此,相关管理部门制定了针对商品质量与服务的评价体系,现从评价系统中选出成功交易200例,并对其评价进行统计:对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)依据题中的数据完成下表,并通过计算说明,能否有99.9%的把握认为“商品好评与服务好评”有关;
(2)若将频率视为概率,某人在该购物平台上进行了5次购物,设对商品和服务全好评的次数为随机变量
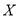 ,求
,求 的分布列(概率用算式表示)、数学期望和方差.
的分布列(概率用算式表示)、数学期望和方差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个四位数的各位数字相加和为
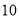 ,则称该数为“完美四位数”,如数字“
,则称该数为“完美四位数”,如数字“ ”.试问用数字
”.试问用数字 组成的无重复数字且大于
组成的无重复数字且大于 的“完美四位数”有( )个
的“完美四位数”有( )个A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
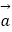 =(m,cos2x),
=(m,cos2x), 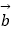 =(sin2x,n),设函数f(x)=
=(sin2x,n),设函数f(x)= 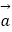
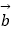 ,且y=f(x)的图象过点(
,且y=f(x)的图象过点( 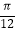 ,
, 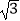 )和点(
)和点( 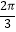 ,﹣2). (Ⅰ)求m,n的值;
,﹣2). (Ⅰ)求m,n的值;
(Ⅱ)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象.若y=g(x)的图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,多面体
 中,四边形
中,四边形 是菱形,
是菱形,  ,
,  相交于
相交于 ,
,  ,点
,点 在平面
在平面 上的射影恰好是线段
上的射影恰好是线段 的中点.
的中点.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)若直线
 与平面
与平面 所成的角为
所成的角为 ,求平面
,求平面 与平面
与平面 所成角(锐角)的余弦值.
所成角(锐角)的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】是否存在实数a,使得函数y=cos2x+asinx+
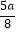 ﹣
﹣  在闭区间[0,π]的最大值是0?若存在,求出对应的a的值;若不存在,试说明理由.
在闭区间[0,π]的最大值是0?若存在,求出对应的a的值;若不存在,试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )

A.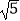
B.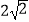
C.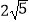
D.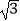
相关试题

