搜索
【题目】如图，三棱柱
中，
，
平面
.
（1）证明：
；
（2）若
，
，求二面角
的余弦值.
参考答案：
【答案】(1)见解析；（2）余弦值为
.
【解析】分析: (1)先证明
平面
,即证
.(2)先证明
,
,再建立空间直角坐标系,利用向量法求二面角
的余弦值.
详解:（1）证明：∵
平面
，∴
.
∵
，
∴
，∴平面，∴.
（2）解：∵平面，∴
，
∴四边形为菱形，∴
.
又
，∴
与
均为正三角形.
取
的中点
，连接
，则.
由（1）知，则可建立如图所示的空间直角坐标系
.
设
，则
，
，
，
，
.
∴
，
，
.
设平面
的法向量为
，
则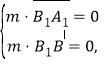
，
∴
∴
取
，则
为平面的一个法向量.
又为平面的一个法向量，
∴
.
又二面角的平面角为钝角，所以其余弦值为
.
点睛:本题主要考查空间位置关系的证明和二面角的平面角的计算,主要考查学生的空间想象能力和计算能力.属于中档题.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某旅游景点有50辆自行车供游客租赁使用，管理这些自行车的费用是每日115元。根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超过6元，则每提高1元，租不出去的自行车就增加3辆.规定：每辆自行车的日租金不超过20元，每辆自行车的日租金
元只取整数，并要求出租所有自行车一日的总收入必须超过一日的管理费用，用
表示出租所有自行车的日净收入（即一日中出租所以自行车的总收入减去管理费用后的所得）.（1）求函数
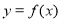的解析式及定义域；（2）试问日净收入最多时每辆自行车的日租金应定为多少元？日净收入最多为多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场按月订购一种家用电暖气，每销售一台获利润200元，未销售的产品返回厂家，每台亏损50元，根据往年的经验，每天的需求量与当天的最低气温有关，如果最低气温位于区间
，需求量为100台；最低气温位于区间
，需求量为200台；最低气温位于区间
，需求量为300台。公司销售部为了确定11月份的订购计划，统计了前三年11月份各天的最低气温数据，得到下面的频数分布表：最低气温(℃)
天数
11
25
36
16
2
以最低气温位于各区间的频率代替最低气温位于该区间的概率.
求11月份这种电暖气每日需求量
(单位：台)的分布列；若公司销售部以每日销售利润
(单位：元)的数学期望为决策依据，计划11月份每日订购200台或250台，两者之中选其一，应选哪个？ -
科目： 来源： 题型：
查看答案和解析>>【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查，随机抽调了50人，他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元)
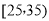
频数
5
10
15
10
5
5
赞成人数
4
8
12
5
2
1
(1)由以上统计数据填下面2×2列联表，并问是否有99％的把握认为“月收入以5500元为分界点对“楼市限购令”的态度有差异；
月收入不低于55百元的人数
月收入低于55百元的人数
合计
赞成
a=______________
c=______________
______________
不赞成
b=______________
d=______________
______________
合计
______________
______________
______________
(2)试求从年收入位于
（单位：百元）的区间段的被调查者中随机抽取2人，恰有1位是赞成者的概率。参考公式：
，其中
.参考值表：
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于函数
，若在定义域内存在实数x，满足
，则称为“局部奇函数”。
为定义在
上的“局部奇函数”；q：曲线
与x轴交于不同的两点。(1)当p为真时，求m的取值范围.
(2)若“
”为真命题，且“
”为假命题，求m的取值范围。 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知倾斜角为
的直线经过抛物线
：
的焦点
，与抛物线相交于
、
两点，且
.（Ⅰ）求抛物线
的方程；（Ⅱ）过点
的两条直线
、
分别交抛物线于点
、
和
、，线段
和
的中点分别为
、
.如果直线与的倾斜角互余，求证：直线
经过一定点.
相关试题
