【题目】已知数列![]() 是等差数列,其前
是等差数列,其前![]() 项和为
项和为![]() ,数列
,数列![]() 是公比大于0的等比数列,且
是公比大于0的等比数列,且![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)令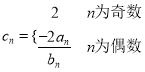 ,求数列
,求数列![]() 的前
的前![]() 项和为
项和为![]() .
.
参考答案:
【答案】(Ⅰ)![]() ,
, ![]() ;(Ⅱ)
;(Ⅱ) 
【解析】试题分析:(Ⅰ)根据题意设数列![]() 的公差为
的公差为![]() ,
, ![]() 的公比为
的公比为![]() ,且
,且![]() ,
,
由![]() ,,解得
,,解得![]() ,
, ![]() ,,则数列
,,则数列![]() 和
和![]() 的通项公式可求;
的通项公式可求;
(Ⅱ)由(Ⅰ)知, ![]() ,
, ![]() ,则
,则
当![]() 为偶数时,奇数项和偶数项各有
为偶数时,奇数项和偶数项各有![]() 项,
项,
∴![]() .
.
令![]() ,利用错位相减法可得
,利用错位相减法可得![]()
故![]() 为偶数时,
为偶数时, ![]() ,
,
当![]() 为奇数时,
为奇数时, ![]() 为偶数,
为偶数,
![]() ,
,
试题解析:(Ⅰ)设数列![]() 的公差为
的公差为![]() ,
, ![]() 的公比为
的公比为![]() ,且
,且![]() ,
,
由题易知, ![]() ,
, ![]() ,
,
由![]() ,得
,得![]() ,
,
解得![]() (
(![]() 舍去),此时
舍去),此时![]() ,
,
∴![]() ,
, ![]() .
.
(Ⅱ)由(Ⅰ)知, ![]() ,
, ![]() ,
,
∴ ,
,
当![]() 为偶数时,奇数项和偶数项各有
为偶数时,奇数项和偶数项各有![]() 项,
项,
∴![]() .
.
令![]() ,
,
∴![]() ,
,
![]() ,
,
以上两式相减得,
![]() ,
,
 .
.
![]()
故![]() 为偶数时,
为偶数时, ![]() ,
,
当![]() 为奇数时,
为奇数时, ![]() 为偶数,
为偶数,
![]() ,
,
经验证, ![]() 也适合上式,
也适合上式,
综上得
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
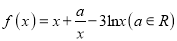 .
.(1)若
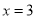 是
是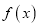 的一个极值点,求
的一个极值点,求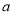 值及
值及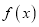 的单调区间;
的单调区间;(2)当
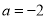 时,求
时,求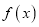 在区间
在区间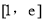 上的最值.
上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
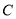 :
: 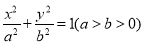 的离心率为
的离心率为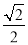 ,点
,点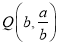 在椭圆上,
在椭圆上, 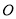 为坐标原点.
为坐标原点.(1)求椭圆
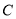 的方程;
的方程; (2)已知点
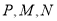 为椭圆
为椭圆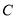 上的三点,若四边形
上的三点,若四边形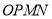 为平行四边形,证明:四边形
为平行四边形,证明:四边形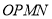 的面积
的面积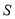 为定值,并求该定值.
为定值,并求该定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
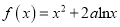 。
。(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)若函数
 在
在 上是减函数,求实数
上是减函数,求实数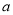 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
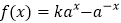 , (a>0且a≠1)是定义域为R的奇函数.
, (a>0且a≠1)是定义域为R的奇函数.(Ⅰ) 求
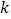 的值
的值 (Ⅱ)若
 ,试求不等式
,试求不等式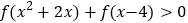 的解集;
的解集;(Ⅲ)若
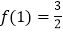 ,且
,且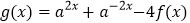 ,求
,求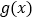 在
在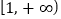 上的最小值。
上的最小值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
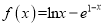 ,
,  .
.(Ⅰ)判断函数
 零点的个数,并说明理由;
零点的个数,并说明理由;(Ⅱ)记
 ,讨论
,讨论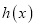 的单调性;
的单调性;(Ⅲ)若
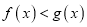 在
在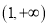 恒成立,求实数
恒成立,求实数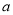 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  .
.(1)求函数
 的极值;
的极值;(2)若函数
 在区间
在区间 内有两个零点,求
内有两个零点,求 的取值范围;
的取值范围;(3)求证:当
 时,
时,  .
.
相关试题

