【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆上,
在椭圆上, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知点![]() 为椭圆
为椭圆![]() 上的三点,若四边形
上的三点,若四边形![]() 为平行四边形,证明:四边形
为平行四边形,证明:四边形![]() 的面积
的面积![]() 为定值,并求该定值.
为定值,并求该定值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由椭圆离心率![]() ,可得
,可得![]() ,将
,将![]() 代入椭圆方程可得
代入椭圆方程可得![]() ,则椭圆方程可求;
,则椭圆方程可求;
(2)分情况讨论,当不存在时, ![]() 方程为:
方程为: ![]() 或
或![]() ,可得
,可得![]() .
.
当直线![]() 的斜率
的斜率![]() 存在时,设直线
存在时,设直线![]() 方程为:
方程为: ![]() ,
, ![]() ,
, ![]() .
.
将![]() 的方程代入
的方程代入![]() 得:
得: ![]() ,可求得
,可求得
![]()
由![]() 得:
得: ![]() ,
,
将![]() 点坐标代入椭圆
点坐标代入椭圆![]() 方程得:
方程得: ![]() .又
.又![]() 到直线
到直线![]() 的距离
的距离![]() ,,最后由
,,最后由
![]() .
.
综上,平行四边形![]() 的面积
的面积![]() 为定值
为定值![]() .
.
试题解析:
(1)由![]() ,得
,得![]() ,
,
将![]() 代入椭圆
代入椭圆![]() 的方程可得
的方程可得![]() ,所以
,所以![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线的斜率![]() 不存在时,
不存在时, ![]() 方程为:
方程为: ![]() 或
或![]() ,
,
从而有![]() ,
,
所以![]() .
.
当直线![]() 的斜率
的斜率![]() 存在时,
存在时,
设直线![]() 方程为:
方程为: ![]() ,
, ![]() ,
, ![]() .
.
将![]() 的方程代入
的方程代入![]() 整理得:
整理得: ![]() ,
,
所以![]() ,
, ![]() ,
,
![]() ,
,
由![]() 得:
得: ![]() ,
,
将![]() 点坐标代入椭圆
点坐标代入椭圆![]() 方程得:
方程得: ![]() .
.
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
![]() ,
,
![]() .
.
综上,平行四边形![]() 的面积
的面积![]() 为定值
为定值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
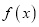 是定义在
是定义在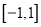 上的奇函数,且
上的奇函数,且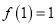 .若对任意的
.若对任意的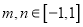 ,
, 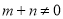 都有
都有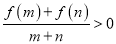 .
.(1)用函数单调性的定义证明:
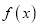 在定义域上为增函数;
在定义域上为增函数;(2)若
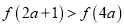 ,求
,求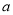 的取值范围;
的取值范围;(3)若不等式
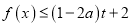 对所有的
对所有的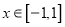 和
和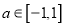 都恒成立,求实数
都恒成立,求实数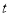 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是定义在R上的二次函数f(x)的部分图像,图2是函数
 的部分图像。
的部分图像。
(Ⅰ) 分别求出函数
 和
和 的解析式;
的解析式;(Ⅱ)如果函数
 在区间
在区间 上是单调递减函数,求
上是单调递减函数,求 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
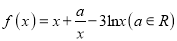 .
.(1)若
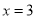 是
是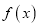 的一个极值点,求
的一个极值点,求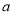 值及
值及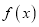 的单调区间;
的单调区间;(2)当
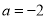 时,求
时,求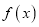 在区间
在区间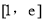 上的最值.
上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
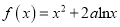 。
。(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)若函数
 在
在 上是减函数,求实数
上是减函数,求实数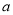 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
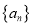 是等差数列,其前
是等差数列,其前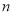 项和为
项和为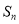 ,数列
,数列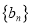 是公比大于0的等比数列,且
是公比大于0的等比数列,且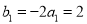 ,
, 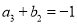 ,
, 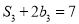 .
.(Ⅰ)求数列
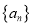 和
和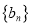 的通项公式;
的通项公式;(Ⅱ)令
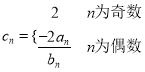 ,求数列
,求数列 的前
的前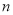 项和为
项和为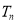 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
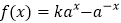 , (a>0且a≠1)是定义域为R的奇函数.
, (a>0且a≠1)是定义域为R的奇函数.(Ⅰ) 求
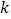 的值
的值 (Ⅱ)若
 ,试求不等式
,试求不等式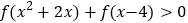 的解集;
的解集;(Ⅲ)若
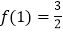 ,且
,且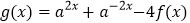 ,求
,求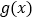 在
在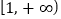 上的最小值。
上的最小值。
相关试题

