【题目】已知椭圆![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=![]() ,连结椭圆的四个顶点得到的菱形的面积为4.
,连结椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设直线l与椭圆相交于不同的两点A,B.已知点A的坐标为(-a,0).若|AB|=![]() ,求直线l的倾斜角.
,求直线l的倾斜角.
参考答案:
【答案】(1)![]() +y2=1(2)
+y2=1(2)![]() 或
或![]()
【解析】(1)由e=![]() =
=![]() ,解得3a2=4c2.再由c2=a2-b2,解得a=2b.
,解得3a2=4c2.再由c2=a2-b2,解得a=2b.
由题意可知![]() ×2a×2b=4,即ab=2.解方程组
×2a×2b=4,即ab=2.解方程组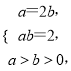 得
得![]()
所以椭圆的方程为![]() +y2=1.
+y2=1.
(2)由(1)可知点A(-2,0),设点B的坐标为(x1,y1),直线l的斜率为k,则直线l的方程为y=k(x+2).于是A、B两点的坐标满足方程组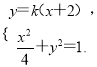
消去y并整理,得(1+4k2)x2+16k2x+(16k2-4)=0,
由-2x1=![]() ,得x1=
,得x1=![]() ,从而y1=
,从而y1=![]() ,
,
故|AB|=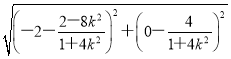 =
=![]() .
.
由|AB|=![]() ,得
,得![]() =
=![]() .整理得32k4-9k2-23=0,
.整理得32k4-9k2-23=0,
即(k2-1)(32k2+23)=0,解得k=±1.所以直线l的倾斜角为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】东亚运动会将于2013年10月6日在天津举行.为了搞好接待工作,组委会打算学习北京奥运会招募大量志愿者的经验,在某学院招募了16名男志愿者和14名女志愿者,调查发现,男女志愿者中分别有10人和6人喜爱运动,其余人不喜欢运动.
(1)根据以上数据完成以下2×2列联表:
喜爱运动
不喜爱运动
总计
男
10
16
女
6
14
总计
30
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少?
参考公式:K2=
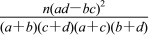 ,其中
,其中n=a+b+c+d.
参考数据:
P(K2≥k)
0.40
0.25
0.10
0.010
k
0.708
1.323
2.706
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
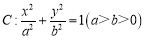 的离心率为
的离心率为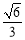 ,以原点
,以原点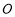 为圆心,椭圆
为圆心,椭圆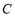 的长半轴长为半径的圆与直线
的长半轴长为半径的圆与直线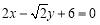 相切.
相切.(Ⅰ)求椭圆
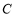 的标准方程;
的标准方程;(Ⅱ)已知点
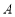 ,
,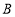 为动直线
为动直线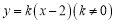 与椭圆
与椭圆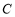 的两个交点,问:在
的两个交点,问:在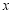 轴上是否存在定点
轴上是否存在定点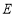 ,使得
,使得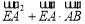 为定值?若存在,试求出点
为定值?若存在,试求出点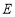 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|2x+1|-|x-4|.
(1)解不等式f(x)>2;
(2)若函数f(x)≥m恒成立,求m的最大整数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在高中学习过程中,同学们经常这样说:“如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的物理和数学成绩,如下表:
编号
成绩
1
2
3
4
5
物理(
 )
)90
85
74
68
63
数学(
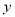 )
)130
125
110
95
90
求数学成绩
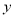 关于物理成绩
关于物理成绩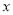 的线性回归方程
的线性回归方程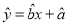 (
(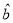 精确到
精确到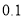
若某位学生的物理成绩为80分,预测他的数学成绩;
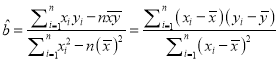
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某上市股票在30天内每股的交易价格
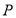 (元)与时间
(元)与时间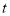 (天)组成有序数对
(天)组成有序数对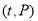 ,点
,点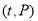 落在图中的两条线段上.
落在图中的两条线段上.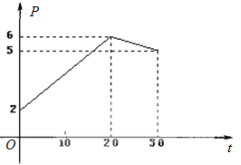
该股票在30天内的日交易量
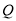 (万股)与时间
(万股)与时间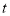 (天)的部分数据如下表所示:
(天)的部分数据如下表所示:第
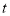 天
天4
10
16
22
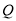 (万股)
(万股)36
30
24
18
(1)根据提供的图象,写出该股票每股交易价格
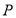 (元)与时间
(元)与时间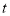 (天)所满足的函数关系式;
(天)所满足的函数关系式;(2)根据表中数据,写出日交易量
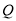 (万股)与时间
(万股)与时间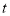 (天)的一次函数关系式;
(天)的一次函数关系式;(3)用
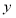 (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出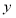 关于
关于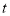 的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
相关试题

