【题目】已知全集U=R,集合A={x|-5<x<5},B={x|0≤x<7},求:(1)A∩B;(2)A∪B;(3)A∪(UB);(4)B∩(UA);(5)(UA)∩(UB).
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;(5)
;(5) ![]()
【解析】试题分析:根据已知及集合间的关系求出![]() ,在数轴上表示集合
,在数轴上表示集合![]() ,就能直观的显示出所示结果,再将结果用数学式表示出来即可.
,就能直观的显示出所示结果,再将结果用数学式表示出来即可.
试题解析:
解:如图①.
(1)A∩B={x|0≤x<5}.
(2) ![]() .
.
![]()
图①
(3)如图②.
![]()
图②
UB={x|x<0,或x≥7},
∴![]() .
.
(4)如图③.
![]()
图③
UA={x|x≤-5,或x≥5},
. ![]()
(5)(方法一)∵UB={x|x<0,或x≥7},
UA={x|x≤-5,或x≥5},
∴如图④.
![]()
图④
(UA)∩(UB)={x|x≤-5,或x≥7}.
(方法二) ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两圆C1:x2+y2-2x-6y-1=0和C2:x2+y2-10x-12y+45=0.
(1)求证:圆C1和圆C2相交;
(2)求圆C1和圆C2的公共弦所在直线的方程和公共弦长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知随机变量
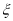 的取值为不大于
的取值为不大于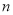 的非负整数值,它的分布列为:
的非负整数值,它的分布列为: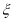
0
1
2
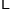
n
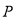
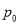
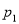
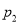
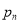
其中
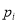 (
(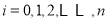 )满足:
)满足: 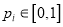 ,且
,且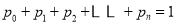 .
.定义由
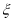 生成的函数
生成的函数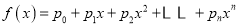 ,令
,令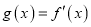 .
.(I)若由
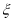 生成的函数
生成的函数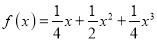 ,求
,求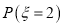 的值;
的值;(II)求证:随机变量
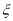 的数学期望
的数学期望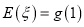 ,
, 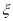 的方差
的方差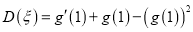 ;
;(
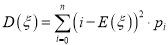 )
)(Ⅲ)现投掷一枚骰子两次,随机变量
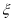 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由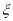 生成的函数记为
生成的函数记为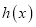 ,求
,求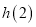 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
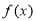 为定义在R上的奇函数,当
为定义在R上的奇函数,当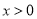 时,
时,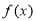 为二次函数,且满足
为二次函数,且满足 ,
,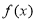 在
在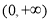 上的两个零点为
上的两个零点为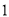 和
和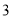 .
.(1)求函数
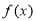 在R上的解析式;
在R上的解析式;(2)作出
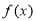 的图象,并根据图象讨论关于
的图象,并根据图象讨论关于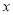 的方程
的方程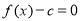
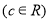 根的个数.
根的个数.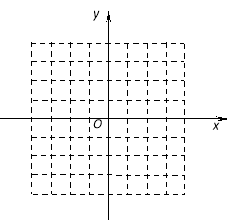
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 .
.(1)求f(2)与f
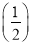 , f(3)与f
, f(3)与f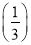 ;
;(2)由(1)中求得结果,你能发现f(x)与f
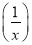 有什么关系?并证明你的发现;
有什么关系?并证明你的发现;(3)求f(1)+f(2)+f(3)+…+f(2013)+f
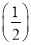 +f
+f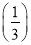 +…+f
+…+f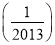 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,知识告知大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”.

(1)求乙班总分超过甲班的概率;
(2)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分,
①请你从平均分和方差的角度来分析两个班的选手的情况;
②主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为
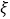 ,求
,求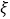 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应市政府“绿色出行”的号召,王老师每个工作日上下班由自驾车改为选择乘坐地铁或骑共享单车这两种方式中的一种出行.根据王老师从2017年3月到2017年5月的出行情况统计可知,王老师每次出行乘坐地铁的概率是0.4,骑共享单车的概率是0.6.乘坐地铁单程所需的费用是3元,骑共享单车单程所需的费用是1元.记王老师在一个工作日内上下班所花费的总交通费用为X元,假设王老师上下班选择出行方式是相互独立的.
(I)求X的分布列和数学期望
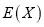 ;
;(II)已知王老师在2017年6月的所有工作日(按22个工作日计)中共花费交通费用110元,请判断王老师6月份的出行规律是否发生明显变化,并依据以下原则说明理由.
原则:设
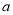 表示王老师某月每个工作日出行的平均费用,若
表示王老师某月每个工作日出行的平均费用,若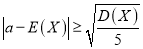 ,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注:
,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注: 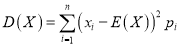 )
)
相关试题

