【题目】如图茎叶图表示的是甲,乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为 . 
参考答案:
【答案】![]()
【解析】解:由已知中的茎叶图可得 甲的5次综合测评中的成绩分别为88,89,90,91,92,
则甲的平均成绩: ![]() (88+89+90+91+92)=90
(88+89+90+91+92)=90
设污损数字为x
则乙的5次综合测评中的成绩分别为83,83,87,99,90+X
则乙的平均成绩: ![]() (83+83+87+99+90+x)=88.4+
(83+83+87+99+90+x)=88.4+ ![]() ,
,
当x=9,甲的平均数<乙的平均数,即乙的平均成绩超过甲的平均成绩的概率为 ![]() ,
,
当x=8,甲的平均数=乙的平均数,即乙的平均成绩不小于均甲的平均成绩的概率为 ![]() ,
,
甲的平均成绩超过乙的平均成绩的概率为1﹣ ![]() =
= ![]()
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解茎叶图(茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少),还要掌握平均数、中位数、众数(⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知常数
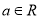 ,解关于
,解关于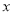 的不等式
的不等式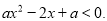
-
科目: 来源: 题型:
查看答案和解析>>【题目】过点A(4,1)的圆C与直线x﹣y﹣1=0相切于点B(2,1),则圆C的方程为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于 .
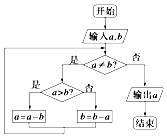
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}中,bn>0(n∈N*),且b1+b2+b3=15,又a1+b1、a2+b2、a3+b3成等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)求数列{an·bn}的前n项和Tn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩
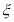 服从正态分布
服从正态分布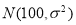 ,已知
,已知 ,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取
,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取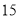 份;
份;②已知命题
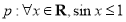 ,则
,则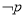 :
: ;
;③在
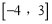 上随机取一个数
上随机取一个数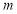 ,能使函数
,能使函数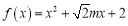 在
在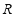 上有零点的概率为
上有零点的概率为 ;
;④设
 ,则“
,则“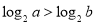 ”是“
”是“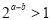 ”的充要条件.
”的充要条件.其中真命题的序号为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线
 的极坐标方程是
的极坐标方程是 ,以极点为原点
,以极点为原点 ,极轴为
,极轴为 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系 中,曲线
中,曲线 的参数方程为:
的参数方程为: (
( 为参数).
为参数).(1)求曲线
 的直角坐标方程与曲线
的直角坐标方程与曲线 的普通方程;
的普通方程;(2)将曲线
 经过伸缩变换
经过伸缩变换 后得到曲线
后得到曲线 ,若
,若 分别是曲线
分别是曲线 和曲线
和曲线 上的动点,求
上的动点,求 的最小值.
的最小值.
相关试题

